△ABC;
AM = MB;
BN = NC;
MN = 4 см.
АС = ? см.
Т.к. отрезок MN соединяет середины сторон треугольника АВС, то этот отрезок - средняя линия.
Исходя из этого, вспоминаем теорему средней линии: средняя линия треугольника параллельна основанию и равна его половине.
Поскольку отрезок MN параллелен основанию AC треугольника ABC и в 2 раза меньше этого основания, то АС = 4 * 2 = 8 см.
Дано:
△ABC; AM = MB; BN = NC; MN = 4
Найти:
АС = ?
Поэтому по теореме средней линии: средняя линия треугольника параллельна основанию и равна его половине.
Значит, MN=*AC, отсюда следует, что АС = 4 * 2 = 8 см.
ответ: АС = 8 см.
△ABC;
AM = MB;
BN = NC;
MN = 4 см.
Найти:АС = ? см.
Решение:Т.к. отрезок MN соединяет середины сторон треугольника АВС, то этот отрезок - средняя линия.
Исходя из этого, вспоминаем теорему средней линии: средняя линия треугольника параллельна основанию и равна его половине.
Поскольку отрезок MN параллелен основанию AC треугольника ABC и в 2 раза меньше этого основания, то АС = 4 * 2 = 8 см.
ответ: АС = 8 см.Дано:
△ABC; AM = MB; BN = NC; MN = 4
Найти:
АС = ?
Т.к. отрезок MN соединяет середины сторон треугольника АВС, то этот отрезок - средняя линия.
Поэтому по теореме средней линии: средняя линия треугольника параллельна основанию и равна его половине.
Значит, MN=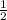 *AC, отсюда следует, что АС = 4 * 2 = 8 см.
*AC, отсюда следует, что АС = 4 * 2 = 8 см.
ответ: АС = 8 см.