Треугольник ABC вписан в окружность с центром O, MB - касательная, точка K - точка пересечения прямой BO с окружностью, угол MBA + угол ACB равен 140 градусам Найти: угол ABK

1) Пусть в одной части х см.

По условию катеты прямоугольного треугольника равны а = 3х см, b = 4х см, тогда по теореме Пифагора гипотенуза этого треугольника равна

с = √(а² + b²) = √(9x² + 16x²) = 5x (см).

2) В прямоугольном треугольнике

r = p - c

p = (3x + 4x + 5x) : 2 = 6x (см).

r = 6x - 5x = x (см).

3) По условию r = 4 см, х = 4 см.

S = 1/2•a•b = 1/2 • 3x • 4x = 6x² = 6•4² = 96 (см²).

4) Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы,

R = 1/2•c = 1/2 • 5 • 4 = 10 (см).

S = πR² = π•10² = 100π (см²).

Объём шара = 52

Объяснение:

Формула объёма шара:

Необходимо найти радиус шара.

У  шара и у цилиндра общий радиус. Основание цилиндра это круг с радиусом R, высота цилиндра равна двум радиусам. Значит объём цилиндра вычисляется по формуле:

где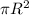 - площадь основания цилиндра,

- высота цилиндра

Подставим объём цилиндра = 78 из условия задачи в данную формулу, и выразим радиус:

Оставим выражение в таком виде, выражать радиус (извлекать корень третьей степени) не обязательно, так как нам понадобится именно R³.

Таким образом, объём шара будет равен: