Бісектриса кута прямокутника ділить його сторону на два відрізки. Один із вiдрiзкiв, який не є стороною утвореного прямокутного трикутника, дорівнює 5 см. Знайти сторони прямокутника, якщо його периметр дорівнює 22 см.
Прямокутником називають такий паралелограм у якого всі кути прямі.
Властивості прямокутника:
У прямокутнику протилежні сторони рівні.
Формула периметру прямокутника має вигляд:
P=2(a+b).
a і b - сторони прямокутника.
Маємо прямокутник ABCD, AB||DC і AD||BC, AЕ – бісектриса. За умовою ЕС=5 см.
Оскільки AЕ – бісектриса, то ∠BAЕ=∠ЕAD.
За ознакою паралельності прямих (AD||BC), як перетнуті січною AЕ, маємо ∠AЕB=∠ЕAD.
Тому ∠BAЕ=∠AЕB. Звідси слідує (за теоремою), що ΔABЕ– рівнобедрений з основою AЕ і бічними сторонами AB і BЕ, тому (за означенням) AB=BЕ= х см.
В правильной четырехугольной призме через середины двух смежных сторон основания проходит плоскость, которая образует с основанием призмы угол α и пересекает три боковых ребра. Найти площадь сечения, если сторона основания призмы А.
Построим сечение.
В основании правильной призмы лежит квадрат.
Отметим середины сторон АВ и AD и поставим точки К и Е соответственно. Соединим их.
Проведем диагонали АС и BD.
КЕ ∩ АС = Н.
Построим угол с вершиной в точке Н, равный α.
НР ∩ СС₁ = М.
Строим сечение, проходящее через три точки.
Продлим КЕ до пересечения с СВ и CD и поставим точки S и N соответственно.
S ∈ BB₁C₁C; M ∈ BB₁C₁C ⇒ S и M соединяем;
SM ∩ BB₁ = X;
N ∈ DD₁C₁C; M ∈ DD₁C₁C ⇒ N и M соединяем;
NM ∩ DD₁ = T;
X ∈ AA₁B₁B; K ∈ AA₁B₁B ⇒ X и K соединяем;
T ∈ AA₁D₁D; E ∈ AA₁D₁D ⇒ T и E соединяем;
EKXMT - искомое сечение.
Сечение представляет пятиугольник, состоящий из трапеции ЕКХТ и треугольника ХМТ.
⇒ S( EKXMT) = S(ЕКХТ) + S(ХМТ)
1. Рассмотрим ΔABD - прямоугольный.
AD = AB = a (условие)
По теореме Пифагора найдем BD:
BD² = AD² + AB² = 2a²
BD = a√2
ЕК - средняя линия ΔАВD.
Средняя линия равна половине длины стороны, которую она не пересекает.
⇒ - меньшее основание ЕКХТ.
2. Рассмотрим ΔНРО - прямоугольный.
∠РНО = α (условие).
Диагонали квадрата равны и точкой пересечения делятся пополам.
⇒
Средняя линия треугольника делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.
⇒
Косинус угла - отношение прилежащего катета к гипотенузе.
- высота ЕКХТ.
ХТ = BD = a√2 - большее основание ЕКХТ.
3. Найдем площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований на высоту.
4. Рассмотрим ΔНМС - прямоугольный.
НС = НО + ОС
Тогда РМ = НМ - НР
5. Найдем площадь ΔХМТ.
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.
Сторони прямокутника: 3 см і 8 см
Объяснение:
Бісектриса кута прямокутника ділить його сторону на два відрізки. Один із вiдрiзкiв, який не є стороною утвореного прямокутного трикутника, дорівнює 5 см. Знайти сторони прямокутника, якщо його периметр дорівнює 22 см.
Прямокутником називають такий паралелограм у якого всі кути прямі.
Властивості прямокутника:
У прямокутнику протилежні сторони рівні.Формула периметру прямокутника має вигляд:
P=2(a+b).a і b - сторони прямокутника.
Маємо прямокутник ABCD, AB||DC і AD||BC, AЕ – бісектриса. За умовою ЕС=5 см.
Оскільки AЕ – бісектриса, то ∠BAЕ=∠ЕAD.
За ознакою паралельності прямих (AD||BC), як перетнуті січною AЕ, маємо ∠AЕB=∠ЕAD.
Тому ∠BAЕ=∠AЕB. Звідси слідує (за теоремою), що ΔABЕ– рівнобедрений з основою AЕ і бічними сторонами AB і BЕ, тому (за означенням) AB=BЕ= х см.
ВС = ВЕ+ЕС = (х + 5) см
Знайдемо периметр паралелограма:
Р = 2*(АВ+ВС) = 2* (х+х+5)=2*(2х+5)
За умовою Р=22см, тому складаємо рівняння:
2*(2х+5)=22
2х+5=11
2х=6
х=3
За властивістю паралелограма:
АВ = CD = х = 3 см
ВС = AD = х+5 =3+5 = 8 см
#SPJ1
Площадь сечения равна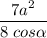 .
.
Объяснение:
В правильной четырехугольной призме через середины двух смежных сторон основания проходит плоскость, которая образует с основанием призмы угол α и пересекает три боковых ребра. Найти площадь сечения, если сторона основания призмы А.
Построим сечение.
В основании правильной призмы лежит квадрат.Отметим середины сторон АВ и AD и поставим точки К и Е соответственно. Соединим их.
Проведем диагонали АС и BD.
КЕ ∩ АС = Н.
Построим угол с вершиной в точке Н, равный α.
НР ∩ СС₁ = М.
Строим сечение, проходящее через три точки.
Продлим КЕ до пересечения с СВ и CD и поставим точки S и N соответственно.
S ∈ BB₁C₁C; M ∈ BB₁C₁C ⇒ S и M соединяем;
SM ∩ BB₁ = X;
N ∈ DD₁C₁C; M ∈ DD₁C₁C ⇒ N и M соединяем;
NM ∩ DD₁ = T;
X ∈ AA₁B₁B; K ∈ AA₁B₁B ⇒ X и K соединяем;
T ∈ AA₁D₁D; E ∈ AA₁D₁D ⇒ T и E соединяем;
EKXMT - искомое сечение.
Сечение представляет пятиугольник, состоящий из трапеции ЕКХТ и треугольника ХМТ.
⇒ S( EKXMT) = S(ЕКХТ) + S(ХМТ)
1. Рассмотрим ΔABD - прямоугольный.
AD = AB = a (условие)
По теореме Пифагора найдем BD:
BD² = AD² + AB² = 2a²
BD = a√2
ЕК - средняя линия ΔАВD.
Средняя линия равна половине длины стороны, которую она не пересекает.⇒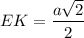 - меньшее основание ЕКХТ.
- меньшее основание ЕКХТ.
2. Рассмотрим ΔНРО - прямоугольный.
∠РНО = α (условие).
Диагонали квадрата равны и точкой пересечения делятся пополам.⇒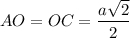
Средняя линия треугольника делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.⇒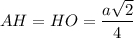
Косинус угла - отношение прилежащего катета к гипотенузе.ХТ = BD = a√2 - большее основание ЕКХТ.
3. Найдем площадь трапеции.
Площадь трапеции равна произведению полусуммы оснований на высоту.4. Рассмотрим ΔНМС - прямоугольный.
НС = НО + ОС
Тогда РМ = НМ - НР
5. Найдем площадь ΔХМТ.
Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.6. Теперь можем найти площадь сечения:
Площадь сечения равна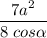 .
.
#SPJ1