Расстояние от точки М до середины стороны квадрата (апофема пирамиды МАВСD) ≈ 11 см
Объяснение:
Дано:
Квадрат АВСD
MA = МВ = МС = MD = 12 см
α = 60°
MАВСD - правильная четырёхугольная пирамида
Найти:
Апофему А пирамиды
Опустим перпендикуляр из точки М на основание АВСD. Он пересечёт основание в точке О. МО - высота пирамиды. ОА - проекция бокового ребра МА пирамиды на основание, поэтому заданный в условии угол α = 60° - угол между боковым ребром МА и его проекцией ОА.
В прямоугольном треугольнике МАО (∠МОА = 90°) найдём катеты ОА и МО
МО = МА · sin α = 12 · sin α = 12 · 0,5√3 = 6√3 (см)
OA = MA · cos α = 12 · cos 60° = 12 · 0.5 = 6 (см)
ОА является половиной диагонали квадрата АВСD.
Сторона квадрата а = 2АО : √2 = 12 : √2 = 6√2 (cм)
Апофему пирамиды найдём, используя теорему Пифагора
треугольник с углами 30° и 120° -это равнобедренный треугольник))
две медианы равнобедренного треугольника (проведенные к боковым сторонам) равны... осталось найти медиану к основанию (m1) и медиану к боковой стороне (m2=m3)
составленный треугольник тоже получится равнобедренным...
его площадь можно найти по формуле Герона...
а можно найти (по теореме косинусов) косинус угла между медианами, найти (используя основное тригонометрическое тождество) синус этог угла и найти площадь по формуле S=0.5ab*sin(x)
1-cos(x) = 1/14
cos(x) = 13/14
sin(x) = √27 / 14
S = (1/2)*(63/4)*(√27 / 14) = 27√3 / 16 (ответ такой же))
Расстояние от точки М до середины стороны квадрата (апофема пирамиды МАВСD) ≈ 11 см
Объяснение:
Дано:
Квадрат АВСD
MA = МВ = МС = MD = 12 см
α = 60°
MАВСD - правильная четырёхугольная пирамида
Найти:
Апофему А пирамиды
Опустим перпендикуляр из точки М на основание АВСD. Он пересечёт основание в точке О. МО - высота пирамиды. ОА - проекция бокового ребра МА пирамиды на основание, поэтому заданный в условии угол α = 60° - угол между боковым ребром МА и его проекцией ОА.
В прямоугольном треугольнике МАО (∠МОА = 90°) найдём катеты ОА и МО
МО = МА · sin α = 12 · sin α = 12 · 0,5√3 = 6√3 (см)
OA = MA · cos α = 12 · cos 60° = 12 · 0.5 = 6 (см)
ОА является половиной диагонали квадрата АВСD.
Сторона квадрата а = 2АО : √2 = 12 : √2 = 6√2 (cм)
Апофему пирамиды найдём, используя теорему Пифагора
А² = МО² + (0,5а)² = (6√3)² + (0,5 · 6√2)² = 108 + 18 = 126 (cм²)
А ≈ 11,22 см
ответ: S=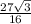
Объяснение:
треугольник с углами 30° и 120° -это равнобедренный треугольник))
две медианы равнобедренного треугольника (проведенные к боковым сторонам) равны... осталось найти медиану к основанию (m1) и медиану к боковой стороне (m2=m3)
составленный треугольник тоже получится равнобедренным...
его площадь можно найти по формуле Герона...
а можно найти (по теореме косинусов) косинус угла между медианами, найти (используя основное тригонометрическое тождество) синус этог угла и найти площадь по формуле S=0.5ab*sin(x)
1-cos(x) = 1/14
cos(x) = 13/14
sin(x) = √27 / 14
S = (1/2)*(63/4)*(√27 / 14) = 27√3 / 16 (ответ такой же))