Укажите номера верных утверждений: 1) если точка пересечения диагоналей трапеции равноудалена от оснований, то эта трапеция является параллелограммом. 2) внешний угол правильного восьмиугольника равен 45. 3) периметр параллелограмма меньше суммы длин его диагоналей. 4) если в параллелограмме диагонали перпендикулярны, то этот параллелограмм является ромбом. 5) центр вписанной окружности правильного пятиугольника является центром симметрии этого пятиугольника. * , желательно с объяснением, просто училка строгая, будет
2. Сумма углов восьмиугольника вычисляется по формуле: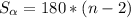
3. Разобьем параллелограмм на четыре треугольника путем проведения в нем диагоналей. Для произвольного треугольника на плоскости всегда выполняется неравенство треугольника: сумма длин двух сторон больше или равна длине третьей. Дальше все понятно, во вложении.
5. У правильного многоугольника с нечентым числом сторон осями симметрии являются прямые, выходящие из вершин углов, которые перпендикулярны противолежащей углам сторонам. Для правильного многоугольника точка пересечения этих прямых будет являться центром описанной окружности. А по свойству тех же правильных многоугольников, это точка будет еще и центром вписанной окружности. Следовательно, центр вписанной окружности является центром симметрии пятиугольника.