Умоляю
1. точка a(4; -2; 5) в центральной симметрии относительно центра c переходит в точку b(-7; 0; -1).
определи координаты точки c .
2. выберите уравнение сферы, симметричной сфере (x−4)2+(y−4)2+(z−2)2=4 относительно точки s(2; 3; −2).
x2+(y−5)2+(z+6)2=2
x2+(y+5)2+(z+6)2=4
(x+4)2+(y+4)2+(z+2)2=4
(x−6)2+(y−7)2+z2=4
x2+(y−2)2+(z+6)2=4
(x−6)2+(y−7)2+z2=2
(x−2)2+(y−1)2+(z−4)2=4
3. в координатной системе дана точка a(6; 6; 1).
определи координаты точек, в которые переходит точка a в…

1. …центральной симметрии относительно начала координат:

2. …осевой симметрии относительно

оси ox:

оси oy:

оси oz:

3 …в зеркальной симметрии относительно

координатной плоскости (xoy):

координатной плоскости (yoz):

координатной плоскости (xoz):

Показать ответ

Ответ:

puh9999

27.03.2021 01:47

Дано:
треугольник АВС
АB = BC
AC - основание
угол ВАС = угол АСВ = 70°
АE - бисс. угла ВАС
СE - бисс. угла ВСА
Найти: углы треугольника АЕС
Решение:
1. Так как АЕ - бисс. угла ВАС, то угол ВАЕ = угол ЕАС. Так как СЕ - бисс. угла ВСА, то угол ВСЕ = угол ЕСА
2. угол ВАЕ + угол ЕАС = угол ВАС
угол ЕАС = 70° / 2 = 35°
3. угол ЕАС = угол ЕСА = 35° (СЕ и АЕ - это бисс. одинаковых углов)
4. угол АЕС + угол ЕАС + угол ЕСА = 180°
угол АЕС = 180° - 35° - 35° = 110°
ответ: угол АЕС = 110°, угол ЕАС = 35°, угол ЕСА = 35°.

0,0(0 оценок)

Ответ:

ABAYMALGAZHDAROvvv

13.08.2021 08:17

Дано: пирамида SABC, SH⊥(ABC), SH = 4 см,

∠ASH=∠CSH=∠BSH=45°, ∠ACB=90°, ∠BAC=30°

Найти : Sбок

Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.

SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°

ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см

SA = SB = SC = 4√2 см

ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см

По теореме Пифагора

AC² = AB² - BC² = 8² - 4² = 48

AC = √48 = 4√3 см

$S_{\Delta ASB}=\dfrac{AB\cdot SH}2=\dfrac {8\cdot 4}2=16$ см²

Площадь двух других граней можно найти по формуле Герона

$S=\sqrt{p(p-a)(p-b)(p-c)}$

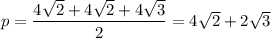
ΔASC, $p=\dfrac{4\sqrt2+4\sqrt2+4\sqrt3}2=4\sqrt2+2\sqrt3$

$S_{\Delta ASC}=\sqrt{(4\sqrt2+2\sqrt3)(4\sqrt2+2\sqrt3-4\sqrt2)(4\sqrt2+2\sqrt3-4\sqrt2)(4\sqrt2+2\sqrt3-4\sqrt3)}=\\\\=\sqrt{(4\sqrt2+2\sqrt3)(2\sqrt3)(2\sqrt3)(4\sqrt2-2\sqrt3)}=\sqrt{(32-12)\cdot 12}=\sqrt{240}\boldsymbol{=4\sqrt{15}}$

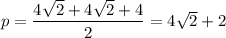
ΔBSC, $p=\dfrac{4\sqrt2+4\sqrt2+4}2=4\sqrt2+2$

$S_{\Delta BSC}=\sqrt{(4\sqrt2+2)(4\sqrt2+2-4\sqrt2)(4\sqrt2+2-4\sqrt2)(4\sqrt2+2-4)}=\\\\=\sqrt{(4\sqrt2+2)\cdot2\cdot2(4\sqrt2-2)}=\sqrt{(32-4)\cdot 4}=\sqrt{28\cdot 4}\boldsymbol{=4\sqrt{7}}$