Геометрия: Упростите выражение 1) АС+BD+DK+NP+CB+KN 2)AC-DB-KN+DK-BC+NP

Упростите выражение 1) АС+BD+DK+NP+CB+KN 2)AC-DB-KN+DK-BC+NP

Показать ответ

Ответ:

Яяяячччч

18.03.2023 19:33

Эту формулу причисляют греческому мудрецу Фалесу (его больше помнят по теореме Фалеса - делению отрезка с любой шкалы и параллельных отрезков). Правда, утверждение звучало по-моему немного иначе: сумма углов треугольника (как минимум прямоугольного) равна сумме двух прямых углов. Но именно оно легло в основу этой теоремы. Фалесу причисляют и определение высоты пирамиды по ее тени. Его труды (около 2300 лет назад) и легли в основу геометрии еще одного грека - Евклида, которая является основой учебника геометрии нашего времени. Как то так :)

0,0(0 оценок)

Ответ:

gavronovaanna2oz9c0h

11.02.2023 21:34

Рассмотрим прямоугольный треугольник SOA в нём радиус описанной окружности основания равен: OA=AB=18. По теореме Пифагора найдем

высоту пирамиды SO.

$SO=\sqrt{SA^2-OA^2}=\sqrt{41^2-18^2} =\sqrt{1357}$

Теперь рассмотрим прямоугольный треугольник SOK. SK - апофема пирамиды, OK - радиус вписанной окружности основания.

OK = AB√3/2 = 9√3

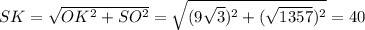
Тогда $SK=\sqrt{OK^2+SO^2}=\sqrt{(9\sqrt{3})^2+(\sqrt{1357})^2}= 40$

Площадь одной грани (треугольник SBA): S = AB*SK/2 = 18*40/2 = 360

Площадь боковой поверхности пирамиды- это сумма всех площадей грани . В шестиугольной пирамиде граней 6, значит площадь боковой поверхности пирамиды равна: Sбок = 6*360 = 2160

ответ: 2160.