В основі піраміди лежить ромб зі стороною a і тупим кутом бета. Дві бічні грані піраміди, що містять сторони цього кута, перпендикулярні до основи, а дві інші - нахилені до неї під кутом альфа. Знайдіть площу повної поверхні піраміди.

Відповідь:

320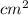

Пояснення:

Площа ромба дорівнює добутку висоти на сторону. Висота ромба дорівнює діаметру вписаного кола, тобто 16 см.

Оскільки АК:КВ=1:4 позначимо АК=х, а КВ=4х. Тоді АВ=4х+х=5х.

Розглянемо трикутник АОВ він прямокутний. І його висота дорівнює 8 см (оскільки діаметр проведений з дотичної К перпендикулярний до сторони АВ). А висота у прямокутному трикутнику дорівнює середньому геометричному між відрізками на які поділяє гіпотенузу. Тобто:

8=

2х=4

х=2

тобто сторона АВ=5*4=20(см)

Отже площа S=16*20=320()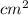

) дуга, ограниченная сторонами угла, являющаяся частью окружности с центром в вершине угла и радиусом 3 см

2) центр описанной около данного треугольника окружности

3) центр вписанной в данный треугольник окружности

4) Если хорда перпендикулярна диаметру, то диаметр проходит через её середину (свойство хорды). 1 : 1

5) в этой задаче не понятно, какой такой угол ОАВ надо найти. По мне так АОВ = 180, ибо эти три точки лежат на одной прямой. О - центр окружности, АВ - диаметр.

если угол между прямыми АВ и СД надо определить, то он равен 90*, по св-ву, указанному в 4)

Подробнее - на -

Объяснение: