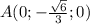В остроугольном треугольнике АВС биссектриса угла А пересекает высоту ВН в точке О , причем ОН = 9 см .Найдите расстояние от точки О до прямой АВ.
2. Один из углов прямоугольного треугольника равен 60 градусов , а сумма гипотенузы и меньшего катета равна 42 см . Найдите длину гипотенузы .
3. Постройте прямоугольный треугольник по гипотенузе и катету.
4. С циркуля и линейки постройте угол равный 150 градусов .
Пусть первая сторона равна x см, тогда вторая равна (x+6) см.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Заметим, что отрезок, образованный биссектрисой и равный 5 см будет находится рядом со большей стороной (т.к 5 см > 3 см). т.е будет прилежать к стороне равной (x+6) см
Исходя из теоремы, приведенной во втором абзаце составим пропорцию:
Решим данное уравнение
Подставим найденное значение x для нахождения сторон треугольника:
Первая сторона: x см = 9 см
Вторая сторона: (x+6) см = (9+6) см = 15 см
Третья сторона состоит из отрезков, на которые она была разбита биссектрисой: 3 см + 5 см = 8 см
ответ: 9 см; 15 см; 8 см
Если сделать рисунок, то будет видно, что точка B лежит в пслокости OXZ, так как ордината точки B равна нулю. Рассмотрим треугольник ABO. Он прямоугольный, одна сторона его OA лежит на оси ординат. Из условия задачи угол ABO=30 градусов (это как раз угол пересечения прямой AB с осью OXZ). Найдем длину OA.
OA=OB*tgABO=OB*tg30
Чтобы найти OA, найдем чему равно OB.
Для этого опустим перпендикуляры из точки B на ось x (пересечение - точка K) и ось z (пересечение - точка L). Из координат точки B понятно, что BK=1, BL=1
Из теоремы Пифагора находим, что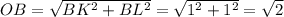
Теперь находим OA:
OA - это и есть значение ординаты точки A
Так как A лежит на оси ординат, ее координаты x=0 и z=0
Возможны два случая:
1) A лежит в положительной части оси ординат
Тогда координаты точки будут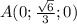
2) A лежит в отрицательной части оси ординат
Тогда координаты точки будут