tg∠FAM = 0,001
Объяснение:
Дано: ∠ACB = 90°, CM = MB, AB = 101, BC = 20,∠CAF = ∠BAF
Найти: tg∠FAM - ?
Решение: Так как по условию угол ∠ACB = 90°, то треугольник ΔACB - прямоугольный, тогда по теореме Пифагора:
Так как по условию CM = MB и CM + MB = CB, то CM = MB = CB : 2 =
= 20 : 2 = 10. Рассмотрим прямоугольный (по условию ∠ACB = 90°) треугольник ΔACM. tg ∠CMA = . CB = CF + FB ⇒ CF =
= CB - FB = 20 - FB. По теореме о биссектрисе для треугольника ΔACB (AF - биссектриса по условию): .
AC * FB = AB * (20 - FB)
99FB = 101(20 - FB)
99FB = 2020 - 101FB
200FB = 2020|:200
FB = 10,1
CF = 20 - FB = 20 - 10,1 = 9,9.
Рассмотрим прямоугольный треугольник ΔACF. tg∠CFA = .
Угол ∠CFA смежный с углом ∠BFA, тогда по свойству смежных углов
∠CFA + ∠BFA = 180° ⇒ ∠BFA = 180° - ∠CFA. Рассмотрим треугольник ΔFAM. По теореме про сумму углов треугольника:
∠FAM + ∠AFM + ∠FMA = 180°;
∠FAM + 180° - ∠CFA + ∠FMA = 180°;
∠FAM = ∠CFA - ∠FMA
tg(∠FAM) = tg(∠CFA - ∠FMA) = .
tg∠FAM = 0,001
Объяснение:
Дано: ∠ACB = 90°, CM = MB, AB = 101, BC = 20,∠CAF = ∠BAF
Найти: tg∠FAM - ?
Решение: Так как по условию угол ∠ACB = 90°, то треугольник ΔACB - прямоугольный, тогда по теореме Пифагора:
Так как по условию CM = MB и CM + MB = CB, то CM = MB = CB : 2 =
= 20 : 2 = 10. Рассмотрим прямоугольный (по условию ∠ACB = 90°) треугольник ΔACM. tg ∠CMA =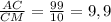 . CB = CF + FB ⇒ CF =
. CB = CF + FB ⇒ CF =
= CB - FB = 20 - FB. По теореме о биссектрисе для треугольника ΔACB (AF - биссектриса по условию): .
.
AC * FB = AB * (20 - FB)
99FB = 101(20 - FB)
99FB = 2020 - 101FB
200FB = 2020|:200
FB = 10,1
CF = 20 - FB = 20 - 10,1 = 9,9.
Рассмотрим прямоугольный треугольник ΔACF. tg∠CFA =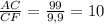 .
.
Угол ∠CFA смежный с углом ∠BFA, тогда по свойству смежных углов
∠CFA + ∠BFA = 180° ⇒ ∠BFA = 180° - ∠CFA. Рассмотрим треугольник ΔFAM. По теореме про сумму углов треугольника:
∠FAM + ∠AFM + ∠FMA = 180°;
∠FAM + 180° - ∠CFA + ∠FMA = 180°;
∠FAM = ∠CFA - ∠FMA
tg(∠FAM) = tg(∠CFA - ∠FMA) =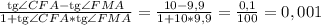 .
.