В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды
Объяснение:
Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.
Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.
S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁= Пусть Р₁К⊥ОР, тогда КР=а- =
Там получается новый треугольник с основанием АД и вершиной С. Треугольник АСД. Найдем сначала угол А. Все мы знаем, что сумма углов треугольника равна 180 градусов. Получаем, что угол С=60, угол В=50, 60+50= 110. 180-110=70. Угол А=70 градусам. По первому закону равенства треугольников (по двум сторонам и углу между ними) мы понимаем, что в полученном треугольнике ВСД угол С равен углу Д. У нас есть точка В с двумя смежными углами, один угол = 50, а второй (т.к. смежный 180-50) равен 130 градусам. В треугольнике ВСД угол В=130 градусам. А по первому закону получается, что С и Д равны, и равны 25 градусам (180-130=50. 50/2=25). Нам дано, что угол С=60, прибавляем еще 25 градусов. Получаем, что угол С в треугольнике АСД теперь равен 85 градусам.
В правильную 4-х угольную усеченную пирамиду вписан куб так, что одна из граней куба совпадает с меньшим основанием усеченной пирамиды , а противоположная грань куба лежит на большем основании усеченной пирамиды . Ребро куба равно a , сторона меньшего основания усеченной пирамиды в 2 раза меньше стороны большего основания .Найдите площадь боковой поверхности усеченной пирамиды
Объяснение:
Т.к. одна из граней куба совпадает с меньшим основанием усеченной пирамиды, то сторона верхнего основания равна а ⇒ сторона большего основания усеченной пирамиды 2а.
Т.к. усеченная пирамида правильная , то боковые грани равнобедренные трапеции.
S( бок. усеч. пир.)=4S( трапеции)=4*1/2*h*(a+2a). Найдем высоту из прямоугольной трапеции ОО₁Р₁Р .
Точка О₁-точка пересечения диагоналей квадрата, поэтому О₁Р₁=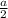 Пусть Р₁К⊥ОР, тогда КР=а-
Пусть Р₁К⊥ОР, тогда КР=а- 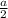 =
=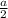
Из ΔКРР₁ по т. Пифагора Р₁К=√(а²+(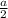 )²)=а√
)²)=а√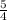 =
=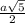 .
.
S( бок. усеч. пир.)=4*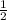 *
*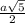 *(a+2a)=3a²√5 (ед²).
*(a+2a)=3a²√5 (ед²).