В равнобедренном треугольнике ABC проведена высота к основанию AC, длина основания равна 21 см, ∡CBD=41°. Trijst_vs1.png Определи длину отрезка AD и величину углов ∡ABD и ∡ABC.
Объяснение:№167 а) ∠8=∠3 (как вертикальные), ∠6-=8, значит ∠6=∠3, а это углы соответственные при прямых а и с и секущей b, значит а║с б)∠5=101°, значит ∠2=101°° (вертикальные),, получается, что∠2=∠7=101°, а это углы соответственные при прямых а и с и секущей b, значит а║с в)∠5+∠8=180° ∠5=∠2 и ∠8=∠3 (как вертикальные), значит∠2+∠3=180°, но это углы односторонние при прямых а и с и секущей b, значит по признаку параллельности прямых а║с г) ∠1+∠7=180° ∠7=∠4 (как вертикальные), значит ∠1+∠4=180° но это углы односторонние при прямых а и с и секущей b, значит по признаку параллельности прямых а║с 2)№198 При пересечении двух параллельных прямых секущей образуется 8 углов. Воспользуемся рис к задаче 1, представив, что а║с. По условию∠1=35°, , значит∠6=35° (вертикальные), ∠1 и ∠2 смежные, значит ∠2=180°-35°=145°, ∠5=135°(вертикальные), ∠3=∠1=35° как накрест лежащие по признаку параллельности прямых, ∠8=∠3 =35°(вертик), ∠8 и ∠7 -смежные, поэтому ∠7=180°-35°=145°, ∠4=∠7=135°(вертик)
№216 По условию АВ║СД, согласно признаку параллельности прямых ∠4= ∠2 =50° как накрест лежащие при параллельных АВ и СД и секущей АС ; аналогично∠5=∠1=70° как накрест лежащие при параллельных АВ и СД и секущей ВС; по сумме улов треугольника ∠3= 180°- (∠4+∠5)=60°
№201 рисунок к задаче не виден , что можно увидеть , выполнено а)∠1=60°, значит ∠6=∠1=60° (как вертикальные) , ∠2 и ∠1 смежные, их сумма равна 180°, значит ∠2= 180°-∠1= 120°, ∠5=∠2=120° (как вертикальные
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Объяснение:№167 а) ∠8=∠3 (как вертикальные), ∠6-=8, значит ∠6=∠3, а это углы соответственные при прямых а и с и секущей b, значит а║с б)∠5=101°, значит ∠2=101°° (вертикальные),, получается, что∠2=∠7=101°, а это углы соответственные при прямых а и с и секущей b, значит а║с в)∠5+∠8=180° ∠5=∠2 и ∠8=∠3 (как вертикальные), значит∠2+∠3=180°, но это углы односторонние при прямых а и с и секущей b, значит по признаку параллельности прямых а║с г) ∠1+∠7=180° ∠7=∠4 (как вертикальные), значит ∠1+∠4=180° но это углы односторонние при прямых а и с и секущей b, значит по признаку параллельности прямых а║с 2)№198 При пересечении двух параллельных прямых секущей образуется 8 углов. Воспользуемся рис к задаче 1, представив, что а║с. По условию∠1=35°, , значит∠6=35° (вертикальные), ∠1 и ∠2 смежные, значит ∠2=180°-35°=145°, ∠5=135°(вертикальные), ∠3=∠1=35° как накрест лежащие по признаку параллельности прямых, ∠8=∠3 =35°(вертик), ∠8 и ∠7 -смежные, поэтому ∠7=180°-35°=145°, ∠4=∠7=135°(вертик)
№216 По условию АВ║СД, согласно признаку параллельности прямых ∠4= ∠2 =50° как накрест лежащие при параллельных АВ и СД и секущей АС ; аналогично∠5=∠1=70° как накрест лежащие при параллельных АВ и СД и секущей ВС; по сумме улов треугольника ∠3= 180°- (∠4+∠5)=60°
№201 рисунок к задаче не виден , что можно увидеть , выполнено а)∠1=60°, значит ∠6=∠1=60° (как вертикальные) , ∠2 и ∠1 смежные, их сумма равна 180°, значит ∠2= 180°-∠1= 120°, ∠5=∠2=120° (как вертикальные
234
Объяснение:
Допустим дана трапеция ABCD, угол ВАС - прямой, биссектриса проведена из угла CDA, АВ=12см, CD=15см. Т.к. биссектриса делит угол пополам, то угол СDB равен углу BDA.
Угол BDA равен углу DBC как накрестлежащий. Следовательно CDB=BDA=DBC. Значит треугольник DBC - равнобедренный и сторона CD равна стороне BC, значит BC=15 см.
Проведем высоту СН к основанию AD. Т.к. трапеция прямоугольная CH=AD=12см. У нас получился прямоугольный треугольник CHD, в котором известно CH=12см, CD=15см.
Нужно найти катет HD.
Используем формулу для нахождения гипотенузы в прямоугольном треугольнике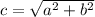
Т.к. ABCH - прямоугольник, то ВС=АH=15см. Из этого следует, что AD=15+9=24. Т.к. трапеция прямоугольная, то сторона AB - высота.
Найдем площадь трапеции по формуле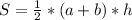
S=1/2*(15+24)*12=6*39=234