, В треугольник ABC вписана окружность с центром О. Луч АО пересекает сторону ВС в точке К. Найдите площадь треугольника ВОС, если АВ=24, АС=30, ВК=13.

1. Известно, что треугольник с искомыми сторонами подобен исходному, то есть все соответственные элементы у треугольников соотносятся как коэффициент подобия.

Пусть коэффициент подобия равен . Тогда стороны второго треугольника равны 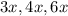. А их сумма, то есть периметр, рана 58,5 см.

Имеем уравнение

ответ: 13,5 см, 18 см, 27 см.

2. Сумма углов треугольника равна 180°. Третий угол равен 180°-(54°+18°)=108°

Далее, биссектриса делит угол пополам, то тупой угол будет разбит на два угла по 108°/2=54°

Получится два треугольника (рисунок приложен)

Рассмотрим треугольник, в котором присутствует угол 18° из исходного треугольника (левый на рисунке). Второй угол равен 54°. Но и в исходном треугольнике есть углы 18° и 54°, а это означает, что этот отсеченный треугольник подобен исходному треугольнику (по двум углам). Второй отсеченный треугольник, кстати, является равнобедренным (имеет два угла по 54°).

В трапеции АВСD. AD⊥AB⊥BC; О - центр вписанной окружности. 

ОС=6, ОD=8.  Найти площадь трапеции. 

_______

Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы его противоположных сторон равны. 

Трапеция - четырехугольник.⇒

АD+BC=AB+CD

Центр вписанной в углы ВСD и СDA окружности лежит на пересечении их биссектрис. ⇒ ∠СОD=90°

По т.Пифагора CD=√(CO²+OD²)=10

Радиус ОН, проведенный в точку касания окружности и боковой стороны - высота ∆ СОD. 

h=2S/CD

ОН=СО•OD:CD=6•8:10=4,8

АВ=2r=9,6=H

AD+BC=9,6+10=19,6

S=H•(AD+BC):2=94,08 (ед. площади)