В треугольнике abc bc/ab = 6 в корне на 2 в корне 3 найдите косинус угла c б

Показать ответ

Ответ:

KittyKittyk

30.12.2020 07:11

1. В прямоугольном треугольнике DCE ∠C = 90°, ∠D = 60°, CE = 3 см. Найдите CD и площадь треугольника.

$S_{DCE} =\frac{CD\cdot CE}{2}$

Нужно найти чему равен катет CD.

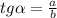1) $tg\alpha =\frac{a}{b}$ , где а — противолежащий катет, b — прилежащий

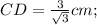
$tg60^{o}=\frac{3}{CD}\\\\\sqrt{3} =\frac{3}{CD}\\\\CD=\frac{3}{\sqrt{3}} (cm)$

Находим площадь ΔDCE:

$S=\frac{3\cdot 3}{2\sqrt{3} } =\frac{9}{2\sqrt{3} } (cm^2)$

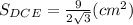
ответ: $CD=\frac{3}{\sqrt{3}} cm;$ $S_{DCE}=\frac{9}{2\sqrt{3}} (cm^2)$

2. В прямоугольном треугольнике PKT ∠T = 90°, KT = 7 см, PT = 7√3 см. Найдите ∠K и гипотенузу треугольника.

По т. Пифагора находим гипотенузу PK:

$PK= \sqrt{PT^2+KT^2}= \sqrt{(7\sqrt{3} )^2+7^2}=\\= \sqrt{49\cdot 3 + 49} = \sqrt{49(3+1)}= \sqrt{49} \cdot \sqrt{4} = 7\cdot 2=14 (cm)$

Находит чему равен ∠K

$sinK=\frac{PT}{KP}\\sinK=\frac{7\sqrt{3} }{14} = \frac{\sqrt{3}}{2} = 60^o$

ответ: PT = 14 см; ∠K = 60°.

3. В равнобедренной трапеции меньшее основание равно 8 см, а высота равна √3 см. Найдите площадь трапеции, если один из ее углов равен 150°.

Обозначим трапецию за ABCD, меньшее основание за BC = 8 см, высоты за BH и BH' = √3 см, ∠B = 150° (при меньшем основании).

BCHH' — прямоугольник, образованный основами и высотами. Отрезки BC = HH' = 8 см.

$S_{ABCD}=\frac{BC+AD}{2}\cdot BH$

Необходимо найти большее основание AD.

Т.к. трапеция равнобокая, угли при основания равны. Сумма углов выпуклого четырехугольника равна 360°. Поэтому сумма углов при большем основании будет равна:

360−(150°+150°) = 360°−300° = 60°

Значит, угол ∠A = ∠D = 60°/2 = 30°

Р-м ΔABH и ΔDCH': прямоугольные, т.к. образованы высотой трапеции; равные, т.к. трапеция ABCD равнобедренная ⇒ AH = DH'.

Отрезок AH выразим с тангенса угла.

$tg30^o=\frac{\sqrt{3} }{AH} ; \frac{1}{\sqrt{3} } =\frac{\sqrt{3} }{AH}\\\\AH=\sqrt{3} \cdot \sqrt{3}=3 (cm)$

Находим длину большего основания:

$AD=AH+DH'+HH'\\AD = 2\cdot 3+ 8 = 6+8=14 (cm)$

Находим площадь трапеции:

$S_{ABCD}= \frac{8+14}{2}\cdot \sqrt{3} = 11\sqrt{3} (cm^2)$

ответ: площадь трапеции 11√3 см².

0,0(0 оценок)

Ответ:

Anastasia934

06.01.2021 23:26

АC = BC

Объяснение:

1) AB||CD, BC - секущая, ∠1 и ∠ABC - накрест лежащие углы. Согласно признаку, если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, делаем вывод что ∠1 = ∠ABC. 2) AB||CD, AC - секущая, ∠2 и ∠BAC - соответственные углы. Согласно признаку, если две параллельные прямые пересечены секущей, то соответственные углы равны, делаем вывод что ∠2 = ∠BAC. 3) Из дано известно, что ∠1 = ∠2 ⇒ ∠ABC = ∠BAC. Согласно свойству, если в треугольнике два угла равны, то треугольник равнобедренный. ⇒ ΔABC - равнобедренный. ⇒ AC = BC.

0,0(0 оценок)

Популярные вопросы: Геометрия