4. Меньшая диагональ ромба равна 12 см, а один из углов - 60°. Найдите вторую диагональ и сторону ромба.
ΔABD равнобедренный (AB = AD как стороны ромба) и ∠BAD = 60°, значит ΔABD равносторонний. Тогда АВ = AD = BD = 12 см.
По свойству параллелограмма сумма квадратов диагоналей равна сумме квадратов сторон параллелограмма: AC² + BD² = 4·AB² AC² = 4·12² - 12² = 3·12² AC = 12√3 см
5. Большее основание и большая боковая сторона прямоугольной трапеции равны а см, а один из углов - 60°. Найдите площадь трапеции.
AD = DC = a см, ∠ADC = 60°, значит ΔADC равносторонний. Проведем высоту трапеции СН. Она является высотой и медианой равностороннего треугольника ADC, тогда СН = а√3/2 см, АН = НD = а/2. СН ║ АВ (как перпендикуляры к одной прямой) и СН = АВ (как высоты трапеции), тогда АВСН - прямоугольник, значит, ВС = АН = а/2 см. Sabcd = (AD + BC)/2 · CH = (a + a/2)/2 · a√3/2 = 3a²√3/8 см²
1) Периметр трапеции ABCD равен 72 см.
2) Углы четырехугольника, вписанного в окружность:
∠A = 10°; ∠B = 165°; ∠C = 170°; ∠D = 15°.
3)Градусная мера дуги, которую отсекает от окружности большее основание трапеции, равна 305°.
Объяснение:
1) Требуется найти периметр прямоугольной трапеции, в которую вписали окружность.
Дано: АВСД - прямоугольная трапеция.
Окр.О,R;
∠D=30°;
ОМ = 6 см.
Найти: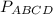 .
.
Для того, чтобы найти периметр, необходимо найти все стороны трапеции.
1. Рассмотрим АВРК.
Радиус, проведенный в точку касания, перпендикулярен касательной.⇒ АВРК - прямоугольник.
AB = 2R = 6*2 = 12 (см)
Противоположные стороны прямоугольника равны.ВР = АК = R = 6 см
2. Рассмотрим ΔНСD - прямоугольный (СН - высота).
∠D = 30°
Катет, лежащий против угла в 30°, равен половине гипотенузы.⇒ CD = 2*CH = 12 * 2 = 24 (см)
3. CD = CE + ED = 24 см.
Отрезки касательных к окружности, проведенные из одной точки, равны.⇒ PC = CE; KD = DE.
или РС + KD = 24 см.
4. Теперь найдем периметр трапеции ABCD.
Периметр - сумма длин всех сторон.= 12 + 6 + 24 +24 + 6 = 72 (см)
Периметр трапеции ABCD равен 72 см.
2) Требуется найди все углы четырехугольника, вписанного в окружность.
Дано: ABCD - вписанный четырехугольник.
∠C + ∠D = 185°; ∠C - ∠D = 155°
Найти: ∠A; ∠B; ∠C; ∠D.
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна 180°.Так нам дана сумма углов, равная 185°, то рассматривать противоположные углы мы не можем. Поэтому выбрали ∠С и ∠D.
1. По условию
∠C + ∠D = 185°
∠C - ∠D = 155°
Сложив эти два уравнения, получим:
2∠С = 340° |:2
∠C = 170°
Подставив это значение в любое из уравнений, получим
∠D = 15°
2. Теперь найдем остальные углы четырехугольника, вписанного в окружность.
∠A + ∠C = 180° ⇒ ∠A = 180° - 170° = 10°
∠B + ∠D = 180° ⇒ ∠B = 180° - 15° = 165°
Углы четырехугольника, вписанного в окружность:
∠A = 10°; ∠B = 165°; ∠C = 170°; ∠D = 15°.
3) Требуется найди градусную меру дуги, которую отсекает от окружности большее основание трапеции.
Дано: Окр.О;
ABCD - трапеция, вписанная в окружность.
∪АВ = 20°; ∪ВС = 15°
Найти: ∪АmD.
Если трапецию можно вписать в окружность, то трапеция – равнобедренная.⇒ ABCD - равнобедренная трапеция, то есть
AB = CD.
Равные хорды стягивают равные дуги.⇒ ∪АВ = ∪CD = 20°
Градусная мера всей окружности равна 360 °.⇒ ∪АmD = 360° - (∪АВ + ∪ВС +∪CD) = 360° - 55° = 305°
Градусная мера дуги, которую отсекает от окружности большее основание трапеции, равна 305°.
Sabcd = a · h₁ Sabcd = b · h₂
12 · h₁ = 72 8 · h₂ = 72
h₁ = 72/12 = 6 см h₂ = 72/8 = 9 см
2. Площадь ромба со стороной 18 см и высотой 7 см равна площади прямоугольника со стороной 14 см. Найдите периметр прямоугольника.
Sabcd = Sklmn
AD · BH = a · b
18 · 7 = 14 · b
b = 18 · 7 / 14 = 9 см
Pklmn = 2(a + b) = 2(14 +9) = 46 см
3. Найдите площадь равнобедренного треугольника, боковая сторона которого равна 15 см, а основание - 24 см.
Проведем ВН - высоту треугольника АВС. Так как треугольник равнобедренный, ВН является медианой.
АН = НС = 24/2 = 12 см
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
ВН = √(АВ² - АН²) = √(225 - 144) = √81 = 9 см
Sabc = AC · BH / 2 = 24 · 9 / 2 = 108 см²
4. Меньшая диагональ ромба равна 12 см, а один из углов - 60°. Найдите вторую диагональ и сторону ромба.
ΔABD равнобедренный (AB = AD как стороны ромба) и ∠BAD = 60°, значит ΔABD равносторонний. Тогда АВ = AD = BD = 12 см.
По свойству параллелограмма сумма квадратов диагоналей равна сумме квадратов сторон параллелограмма:
AC² + BD² = 4·AB²
AC² = 4·12² - 12² = 3·12²
AC = 12√3 см
5. Большее основание и большая боковая сторона прямоугольной трапеции равны а см, а один из углов - 60°. Найдите площадь трапеции.
AD = DC = a см, ∠ADC = 60°, значит ΔADC равносторонний.
Проведем высоту трапеции СН. Она является высотой и медианой равностороннего треугольника ADC, тогда СН = а√3/2 см, АН = НD = а/2.
СН ║ АВ (как перпендикуляры к одной прямой) и СН = АВ (как высоты трапеции), тогда АВСН - прямоугольник, значит, ВС = АН = а/2 см.
Sabcd = (AD + BC)/2 · CH = (a + a/2)/2 · a√3/2 = 3a²√3/8 см²