1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках , но х=20-у ⇒
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Обозначим BC за x. По теореме синусов sin<a/BC=sin<b/AB=sin<c/AC. sin<c=sin<90=1, из чего следует, что AB/sin<90=25/1 равно sin<a/BC=0,6/x. Найдем x по пропорции: x=25*0,6=15.
По теореме Пифагора найдем сторону AC: AC^2=AB^2-BC^2=25^2-15^2=625-225=400; AC=20.
Площадь прямоугольного треугольника находится по формуле AC*BC/2. S=15*20/2=300/2=150.
Площадь любого треугольника можно найти по формуле A*H/2, где A-сторона, а H-опущенная на нее высота. В нашем случае S=AB*CH/2. Выразим CH: CH=S*2/AB; CH=150*2/25=300/25=12.
1.) Стороны данного острого угла параллельны плоскости α. Докажите, что и биссектриса параллельна этой плоскости.
2. Прямые a i b которые пересекаются, пересекают три данные параллельные плоскости α, β, γ в точках А₁,А₂,А₃ и В₁,В₂,В₃ соответственно. Найти B₁B₃ ,если А₁А₂=25см, В₂В₃=4 см,А₂А₃+В₁В₂=20 см (на фото рисунок к задачи).
Объяснение:
1)Стороны острого угла определяют плоскость β единственным образом как и пересекающиеся прямые.И эта плоскость β║α ⇒ все прямые плоскости β параллельны α и значит биссектриса угла параллельна α.
2)Пересекающиеся прямы а и в определяют плоскость , которая пересекает плоскости α, β, γ , единственным образом. Линии пересечения плоскостей будут параллельны , т.е. А₁В₁║А₂В₂║А₃В₃ . Введем для простоты записей обозначения А₂А₃=х , В₁В₂=у , тогда х+у=20.
По т. о пропорциональных отрезках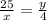
, но х=20-у ⇒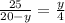 
, y²-20y+100=0 ,(y-10)²=0 ,y=10
B₁B₃ =B₁B₂+В₂В₃=10+4=14 (cм)
==============================
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
CH=12
Объяснение:
Обозначим BC за x. По теореме синусов sin<a/BC=sin<b/AB=sin<c/AC. sin<c=sin<90=1, из чего следует, что AB/sin<90=25/1 равно sin<a/BC=0,6/x. Найдем x по пропорции: x=25*0,6=15.
По теореме Пифагора найдем сторону AC: AC^2=AB^2-BC^2=25^2-15^2=625-225=400; AC=20.
Площадь прямоугольного треугольника находится по формуле AC*BC/2. S=15*20/2=300/2=150.
Площадь любого треугольника можно найти по формуле A*H/2, где A-сторона, а H-опущенная на нее высота. В нашем случае S=AB*CH/2. Выразим CH: CH=S*2/AB; CH=150*2/25=300/25=12.
ответ: 12