Визнач площу перерізу циліндра площиною, паралельної осі циліндра, що знаходиться у відстані 7 од.вим. від осі, якщо висота циліндра дорівнює 22 од.вим., а радіус циліндра дорівнює 25 од.вим.

Показать ответ

Ответ:

BAMBELBI013

18.05.2023 14:45

На рисунке изображена прямоугольная трапеция ABCD, в которую вписан круг. Точка касания окружности делит большую боковую сторону на отрезки длиной 4 см и 25 см. Установите соответствие между началом предложения (1 - 4) и его окончанием (а-д) так, чтобы образовалось правильное утверждение

1 Средняя линия трапеции равна ,2 Высота трапеции равна , 3 радиус вписанной окружности равен , 4 Меньшая диагональ трапеции равна

A )√ 594 см , Б) 20 см, В)2√149 см , Г) 10 см , Д) 24,5 см

Объяснение:

1) Найдем радиус вписанной окружности r=√(CH*HD)=√(4*25)10 (cм)⇒

диаметр ,равный высоте трапеции , равен 2*10=20( см), h=20 cм.

2)Высота прямоугольной трапеции равна меньшей боковой стороне ⇒ АВ=20 см.

3)Суммы противоположных сторон любого четырёхугольника описанного около окружности равны : АВ+CD=BC+AD ⇒BC+AD=20+29=49 (см)

По определению средней линии трапеции имеем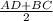 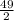$\frac{AD+BC}{2}$ = $\frac{49}{2}$ =24,5(см)

4) Меньшей диагональю будет АС.

По свойству отрезков касательных СН=СК=4 см, ВМ=ВК=10 см, тогда ВС=4+10=14 (см)

ΔАВС-прямоугольный по т. Пифагора АС=√(14²+20²)=√596=√(4*149)=2√149 ( см).

ответ . 1-Д ; 2-Б ; 3-Г ; 4-В .

ів, дуже треба На рисунку зображено прямокутну трапецію ABCD, у яку вписано коло. Точка дотику кола

0,0(0 оценок)

Ответ:

kitti1936

13.01.2021 20:16

1) 3

2) Р = АВ + АС + ВС; ∆АВС - равнобедренный, следовательно АС = ВС.

Значит Р = АВ + 2АС

АС = (Р - АВ) : 2 = (28 - 10) : 2 = 18 : 2 = 9 (см)

ответ: 9 см

3) 1. <А = <В, значит ∆АВС - равнобедренный по признаку равнобедренного треугольника, следовательно АС = ВС

2. пусть х - коэффициент пропорциональности, тогда АВ = 5х, АС = ВС = 2х. Зная, что периметр треугольника 36 см, составляем уравнение:

5х + 2х + 2х = 36

9х = 36

х = 4

АС = 5х = 5 × 4 = 20 (см)

ответ: 20 см

4) 1.∆АВС - равнобедренный, значит <АВС = <АСВ по свойству углов равнобедренного треугольника

2. <ОВС = 1/2<АВС так как ВО - биссектриса, <ОСВ = 1/2<АСВ так как СО - биссектриса. <АВС = <АСВ, значит <ОВС = <ОСВ, следовательно ∆ВОС - равнобедренный по признаку равнобедренного треугольника.

Что и требовалось доказать.

5 1) 12 вроде

5 2)

1. <СВК = 1/2<АВС = 1/2 × 100° = 50° так как ВК - биссектриса

2. <СВК = <С = 50°, следовательно ∆КВС - равнобедренный по признаку равнобедренного треугольника, значит КВ = КС = 6 по свойству сторон равнобедренного треугольника

ответ: 6

0,0(0 оценок)

Популярные вопросы: Геометрия