Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника:
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: .
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны:
Формула вычисления любой стороны прямоугольника, зная диагональ:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то треугольники подобны.
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ . Доказать: ΔАВС подобен ΔА₁В₁С₁. Доказательство: Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) . Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках: АВ₂ : А₁В₁ = АС : А₁С₁. Сравним полученную пропорцию с данной в условии: АВ : А₁В₁ = АС : А₁С₁ Значит, АВ₂ = АВ. Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию). Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит ΔАВС подобен ΔА₁В₁С₁. Доказано.
10.
Как показано на рисунке 611 — AF == AD = AD/2; BC == AF == FD = AD/2.
Теорема такова: если отрезок, проведённый из двух сторон — равен половине третьей стороны, то этот отрезок — средняя линия.
Как мы видим, на стороне AM, центр — B, на стороне AD, центр — F, а на стороне MD, центр — C. Тоесть отезок FC — проведён с центров двух сторон, тоесть — она средняя линия.
Отметим ещё то, что средняя линия параллельна своей противоположной стороне(факт), тоесть: BC║AD.
FC — также средняя линия, тоесть — она равна половине своей противоположной стороны, тоесть: AM = 10 ⇒ CF = 10/2 = 5.
Вывод: CF = 5.
1.
Теорема о 30-градусном угле такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы.
Тоесть: BC = AB/2 ⇒ BC = 4.
Для вычисления площади прямоугольного треугольника — нам надо знать 2 катета(гипотенуза к чёрту не нужна).
А чтобы найти катет AC — зная первый катет, и гипотенузу — используем простейшую теорему Пифагора:
Формула вычисления площади прямоугольного треугольника: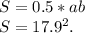
Внимание! Эта формула работает только с прямоугольным треугольником, так как прямоугольный треугольник имеет один прямой угол.
Вычисление площади обычного произвольного треугольника — содержит альтернативную формулу!
2.
Так как один из острых углов равен 45°, то второй острый угол равен: 90-45 = 45° ⇒ <M == <N = 45° ⇒ KM == KN = 4.
Зная 2 катета — найдём гипотенузу NM:
Вывод: NM = 5.66.
3.
Формула вычисления боковой стороны, зная угол, противолежащий основанию, и основание: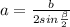 .
.
4.
Формула вычисления биссектрисы, проведённую через острый угол в прямоугольном треугольнике такова:
5.
Формула вычисления диагонали CD — зная 2 стороны: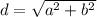
Формула вычисления любой стороны прямоугольника, зная диагональ: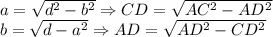
Формула вычисления площади прямоугольника: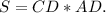
Дано: ∠А = ∠А₁; АВ : А₁В₁ = АС : А₁С₁ .
Доказать: ΔАВС подобен ΔА₁В₁С₁.
Доказательство:
Достроим на стороне АС треугольник АВ₂С, в котором углы, прилежащие к стороне АС, равны углам в треугольнике А₁В₁С₁ (как на рисунке) .
Тогда ΔАВ₂С подобен ΔА₁В₁С₁ по двум углам. Запишем отношение сторон в этих треугольниках:
АВ₂ : А₁В₁ = АС : А₁С₁.
Сравним полученную пропорцию с данной в условии:
АВ : А₁В₁ = АС : А₁С₁
Значит, АВ₂ = АВ.
Но тогда ΔАВС = ΔАВ₂С по двум сторона и углу между ними (АС - общая, АВ₂ = АВ и ∠А = ∠А₁ = ∠1 по условию).
Итак, ΔАВС = ΔАВ₂С, а ΔАВ₂С подобен ΔА₁В₁С₁, значит
ΔАВС подобен ΔА₁В₁С₁.
Доказано.