См. рисунок в приложении Пусть ребро АА₁ образует со сторонами основания АВ и AD угол в 60°. Соединяем точку А₁ с точкой D. В треугольнике АА₁D AA₁=2 м AD=1 м ∠A₁AD=60° По теореме косинусов A₁D²=AA₁²+AD²-2·AA·₁AD·cos60°=4+1-2·2·1(1/2)=3 A₁D=√3 м Треугольник A₁AD- прямоугольный по теореме обратной теореме Пифагора: АА₁²=AD²+A₁D² 2²=1+( √3 )² A₁D⊥AD В основании квадрат, стороны квадрата взаимно перпендикулярны АС⊥AD Отсюда AD⊥ плоскости A₁CD ВС || AD BC ⊥ плоскости A₁CD
ВС⊥A₁C
A₁C перпендикулярна двум пересекающимся прямым ВС и СD плоскости АВСD По признаку перпендикулярности прямой и плоскости А₁С перпендикуляр к плоскости АВСD A₁C - высота призмы A₁C=Н Из прямоугольного треугольника A₁DC: А₁С²=А₁D²-DC²=(√3)²-1=3-1=2 A₁C=Н=√2 м
4)
Так как треугольник равнобедренный, то углы при основании — равны.
И так как каждый из них равен 62°, то угол, противолежащий основанию — равен: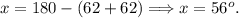
//Надо заметить, что сумма внутренних углов треугольника — всегда равна 180°.//
5)
Чтобы треугольник существовал, сумма каждых двух сторон — должна быть больше каждой оставшийся стороны, тоесть:
Проверим: 7.2+4.3 = 11.5.
Третья сторона не должна быть равна, или больше чила 11.5, тоесть длина оставшийся стороны может максимально равна: 11.499999.
6)
//Нет рисунка//
7) Один из углов треугольника три раза меньше второго и на 150 больше третий. Найдите углы треугольника.
Объявим этот же угол — как переменная "x".
Второй угол, который больше "x" в 3 раза — будет объявлен как: "3x";
Третий угол, который меньше "x" на 150° — будет объявлен как" "x-150".
Составим уравнение:
Как мы видим — один из углов больше суммы всех углов треугольника, а другой-то вообще — отрицательный.
Я опробовала много вариантов, спобом подборки, всё равно не получилось найти целые — соответствующие углам треугольника числа.
Или задача с ошибков, или вот — правильный ответ: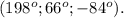
8) Внешний угол равен 105°, что и означает, что внутренний и смежной с ним углов равен: 180-105 = 75°.
По теореме внешнего угла: сумма двух оставшихся внутренних углов, не смежных со внешним углом — равен этому же внешнему углу.
Тоесть сумма двух оставшихся углов равна: x+y = 105°.
Так как их отношения равно — 4:3, то переменные таковы: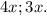
Составим уравнение:
Пусть ребро АА₁ образует со сторонами основания АВ и AD угол в 60°.
Соединяем точку А₁ с точкой D.
В треугольнике АА₁D
AA₁=2 м
AD=1 м
∠A₁AD=60°
По теореме косинусов A₁D²=AA₁²+AD²-2·AA·₁AD·cos60°=4+1-2·2·1(1/2)=3
A₁D=√3 м
Треугольник A₁AD- прямоугольный
по теореме обратной теореме Пифагора:
АА₁²=AD²+A₁D² 2²=1+( √3 )²
A₁D⊥AD
В основании квадрат, стороны квадрата взаимно перпендикулярны
АС⊥AD
Отсюда AD⊥ плоскости A₁CD
ВС || AD
BC ⊥ плоскости A₁CD
ВС⊥A₁C
A₁C перпендикулярна двум пересекающимся прямым ВС и СD плоскости АВСD
По признаку перпендикулярности прямой и плоскости А₁С перпендикуляр к плоскости АВСD
A₁C - высота призмы
A₁C=Н
Из прямоугольного треугольника
A₁DC:
А₁С²=А₁D²-DC²=(√3)²-1=3-1=2
A₁C=Н=√2 м
S(параллелепипеда)=S(осн)·Н=АВ²·Н=1·√2=√2 куб. м