Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна m
Объяснение:
1) Пусть МА=МВ=m -образующие конуса, МО-высота конуса, МО⊥(АОВ) АВ-хорда , ∠АОВ=β. Проведем ОН⊥АВ , тогда МН⊥АВ , по т. о трех перпендикулярах ⇒ ∠МНО-линейный угол между основанием и плоскостью (АВМ), ∠МНО=α .
2) S(бок.конуса )= π * r* l . где r-радиус основания, l-образующая конуса. По условию l =m . Найдем r.
3)В равнобедренном ΔАОВ, высота является биссектрисой ⇒∠АОН=β/2. Получили ΔАОН- прямоугольный :
,
.
4) ΔMHO- прямоугольный : или .
5) ΔAMH- прямоугольный ,по т. Пифагора НА²+МН²=МА² ,
Через две образующие конуса проведена плоскость, которая наклонена к основанию под углом углом α. Эта плоскость пересекает основание конуса по хорде, которая видна из центра основания под углом β. Найдите площадь боковой поверхности конуса, если его образующая равна m
Объяснение:
1) Пусть МА=МВ=m -образующие конуса, МО-высота конуса, МО⊥(АОВ) АВ-хорда , ∠АОВ=β. Проведем ОН⊥АВ , тогда МН⊥АВ , по т. о трех перпендикулярах ⇒ ∠МНО-линейный угол между основанием и плоскостью (АВМ), ∠МНО=α .
2) S(бок.конуса )= π * r* l . где r-радиус основания, l-образующая конуса. По условию l =m . Найдем r.
3)В равнобедренном ΔАОВ, высота является биссектрисой ⇒∠АОН=β/2. Получили ΔАОН- прямоугольный :
4) ΔMHO- прямоугольный :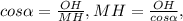 или
или 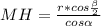 .
.
5) ΔAMH- прямоугольный ,по т. Пифагора НА²+МН²=МА² ,
r =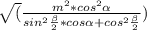 =
= 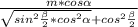 .
.
6) S(бок.конуса )= π *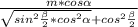 *m
*m
S(бок.конуса )=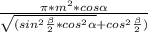 ( ед²) .
( ед²) .
Пусть AB=2, BE=1 => AE =√5 (т Пифагора)
△AKE - равнобедренный, KH - высота и медиана
AH=AE/2 =√5/2
△AYH~△AEB (∠EAD=∠AEB, накрест лежащие)
AY/AE =AH/BE => AY =√5*√5/2*1 =5/2
DY =AY-AD =5/2 -2 =1/2
EC||AD, EC=AD/2 => EC - средняя линия в AXD
E и С - середины AX и XD
Теорема Менелая
AH/HX *XK/KD *DY/YA =1
1/3 *XK/KD *1/5 =1 => XK/KD =15/1
KD=x, XD=16x, CD=8x => CK/KD=7/1
Или
x^2 +a^2/4 = y^2 +a^2 => |:y^2
(x/y)^2 = 1 +3/4 (a/y)^2
x+y =a => |:y
x/y +1 =a/y
k= x/y
k^2 =1 +3/4 (k+1)^2 =>
4k^2 =4 +3(k^2 +2k +1) =>
k^2 -6k -7 =0 =>
k = 3+√(9+7) =7 (k>0)
ответ: x/y =7/1