Рассмотрим треугольник АВС. Он равнобедренный по условию, так как боковые стороны у него равны. Значит, углы при основании тоже равны - по свойству равнобедренного треугольника.
Так как по условию треугольник АВС ещё и прямоугольный, то сумма его острых углов даёт 90° - по свойству прямоугольного треугольника.
Найдем углы при основании:
BAC = ACB = 90° : 2 = 45°.
Далее рассмотрим углы АСВ и ЕСD - они вертикальные, значит АСВ = ЕСD = 45°.
Так как треугольник СЕD по условию тоже равнобедренный (боковые стороны у него равны по условию), то углы при основании равны. Отсюда находим угол СЕD, он же угол х:
Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: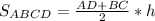
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
ответ: h = 24 см
P.S. Рисунок показан внизу↓
Рассмотрим треугольник АВС. Он равнобедренный по условию, так как боковые стороны у него равны. Значит, углы при основании тоже равны - по свойству равнобедренного треугольника.
Так как по условию треугольник АВС ещё и прямоугольный, то сумма его острых углов даёт 90° - по свойству прямоугольного треугольника.
Найдем углы при основании:
BAC = ACB = 90° : 2 = 45°.
Далее рассмотрим углы АСВ и ЕСD - они вертикальные, значит АСВ = ЕСD = 45°.
Так как треугольник СЕD по условию тоже равнобедренный (боковые стороны у него равны по условию), то углы при основании равны. Отсюда находим угол СЕD, он же угол х:
(180° - угол ЕСD) : 2
(180° - 45°) : 2 = 67,5° - угол х.