Задание 1 ( ). Две стороны треугольника равны 12 см и 6 см, а косинус угла между ними равен 1.png.
Найдите площадь этого треугольника.
Задание 2 ( ).
В треугольнике ABC проведена высота BD, равная 12 см. Найдите площадь треугольника ABC, если ∠ABD = 30°, ∠BCD = 45°.
Задание 3 ( ).
Три окружности попарно касаются друг друга. Радиусы окружностей равны 3 см, 8 см, 22 см. Найдите площадь треугольника, вершинами которого являются центры этих окружностей.
Задание 4 ( ).
Площадь треугольника ABC равна 48 см2. На стороне AC отметили точку N так, что AN : NC = 1 : 5. Найдите площадь треугольника NBC.
Задание 5.
В равнобедренном треугольнике ABC основание AC = 12 см. BM – медиана, равная 8 см. Найдите:
а) радиус вписанной окружности ( );
б) радиус описанной окружности ( ).
кут E=120°
кут F=120°
кут N=60°
кут F=60°
Объяснение:
эта трапеция равнобедренная (NE=FM), это можно сказать ещё с условия задачи
точкой O я пометила точку пересечения EM и NF
они являются диагонали, бисектрисами и и высотами
кут NOM равен 120° за условием, значит кут EOF тоже равен 120° (как вертикальные куты), а кут EON равен 60°
рассмотрим треугольник NOM
в нём кут N=M=(180°-120°)/2=30°
рассмотрим треугольник EOF
в нём кут E=куту F=(180°-120°)/2=30°
рассмотрим треугольник NEO
в треугольнику NEO кут E=90°
значит треугольник прямоугольный
кут O=60°
кут N=30°
продолжим рассматривать трапецию
в ней кут N=куту M=кут ENO+кут ONM=30°+30°=60°
кут E=куту F=кут NEO+кут OEF=90°+30°=120°
KK₁ = 3 ед.
Объяснение:
Дано: прямая АВ;
АК=КВ;
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ.
АА₁ = 5; ВВ₁ = 11.
Найти: КК₁
Пусть А₁В₁= 2а.
Если две прямые перпендикулярны третьей, то они параллельны между собой.
АА₁ ⊥ АВ; ВВ₁ ⊥ АВ; КК₁ ⊥ АВ ⇒ АА₁ || ВВ₁ || КК₁.
Теорема Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
АК = КВ ⇒ А₁К₁ = К₁В₁ = а.
Рассмотрим ΔА₁АО и ΔОВВ₁ - прямоугольные.
Вертикальные угла равны.
∠1 = ∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔОВВ₁ (по двум углам)
Составим пропорцию:
Пусть А₁О = 5х, тогда ОВ₁ = 11х
Составим уравнение:
⇒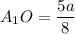
Тогда
Рассмотрим ΔА₁АО и ΔК₁КО - прямоугольные.
∠1=∠2 (вертикальные)
⇒ ΔА₁АО ~ ΔК₁КО
Составим пропорцию: