35°, 52°, 92°
Объяснение:
1) <BOC = 70°, => <BAC = 70° : 2 = 35° по свойству вписанного угла.
Т.к. <BOC = 70°, то дуга BC = 70° тоже по свойству центрального угла, тогда на дуга BAC = 360° - 70° = 290°.
2) По условию AB : AC = 4:7, => дуга AB + дуга AC = 4x + 7x = 290°
11x = 290°
x = 290 : 11 = 26 °
3) Дуга AB = 4x = 4*26 = 105 , => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105 : 2 = 52°
4) Дуга AC = 7x = 7*26 = 184 , => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184 : 2 = 92°
АВ = ВС = АС = 4; ∠А = ∠В = ∠С =60°.
По теореме синусов найдём ∠АВМ.
АМ : sin ∠АВМ = 2√3 : sin 60°
(4:2) : sin ∠АВМ = 2√3 : √3/2
sin ∠АВМ = 1/2,
следовательно, ∠АВМ = 30°.
В Δ АВМ ∠АМВ = 180 - 60 - 30 = 90 °; следовательно треугольник АВМ является прямоугольным, а катет АМ, лежащий против угла 30°, равен 1/2 АВ, откуда АВ = 2 · 2 = 4.
По теореме Пифагора находим ВС = 4
ВС = √(2² + (2√3)² = √16 = 4.
В равностороннем треугольнике все углы равны 60°.
ответ: АВ = ВС = АС = 4; ∠А = ∠В = ∠С =60°.
35°, 52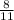 °, 92
°, 92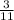 °
°
Объяснение:
1) <BOC = 70°, => <BAC = 70° : 2 = 35° по свойству вписанного угла.
Т.к. <BOC = 70°, то дуга BC = 70° тоже по свойству центрального угла, тогда на дуга BAC = 360° - 70° = 290°.
2) По условию AB : AC = 4:7, => дуга AB + дуга AC = 4x + 7x = 290°
11x = 290°
x = 290 : 11 = 26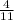 °
°
3) Дуга AB = 4x = 4*26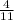 = 105
= 105 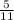 , => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105
, => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105 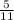 : 2 = 52
: 2 = 52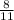 °
°
4) Дуга AC = 7x = 7*26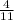 = 184
= 184 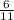 , => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184
, => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184 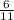 : 2 = 92
: 2 = 92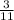 °
°
АВ = ВС = АС = 4; ∠А = ∠В = ∠С =60°.
Объяснение:
По теореме синусов найдём ∠АВМ.
АМ : sin ∠АВМ = 2√3 : sin 60°
(4:2) : sin ∠АВМ = 2√3 : √3/2
sin ∠АВМ = 1/2,
следовательно, ∠АВМ = 30°.
В Δ АВМ ∠АМВ = 180 - 60 - 30 = 90 °; следовательно треугольник АВМ является прямоугольным, а катет АМ, лежащий против угла 30°, равен 1/2 АВ, откуда АВ = 2 · 2 = 4.
По теореме Пифагора находим ВС = 4
ВС = √(2² + (2√3)² = √16 = 4.
В равностороннем треугольнике все углы равны 60°.
ответ: АВ = ВС = АС = 4; ∠А = ∠В = ∠С =60°.