Задан вектор a(2;-4) и точка A (−6; 2). Запишите уравнения прямой, проходящей через точку A, если:
б) вектор a является вектором нормали.
Если известна некоторая точка M(xo; yo), принадлежащая прямой, и вектор нормали n(n1; n2) этой прямой, то уравнение данной прямой выражается формулой:
n1*(x – xo) + n2(y – yo) = 0.
Подставим данные в формулу.
2(x+ 6) - 4(y - 2) = 0, раскроем скобки.
2x + 12 - 4y + 8 = 0 и получаем общий вид уравнения:
2x - 4y + 20 = 0 можно сократить на 2:
x - 2y + 10 = 0.
б) если вектор нормали , то уравнение прямой имеет
вид: .
a) если вектор - это направляющий вектор , то каноническое уравнение прямой имеет вид:
Задан вектор a(2;-4) и точка A (−6; 2). Запишите уравнения прямой, проходящей через точку A, если:
б) вектор a является вектором нормали.
Если известна некоторая точка M(xo; yo), принадлежащая прямой, и вектор нормали n(n1; n2) этой прямой, то уравнение данной прямой выражается формулой:
n1*(x – xo) + n2(y – yo) = 0.
Подставим данные в формулу.
2(x+ 6) - 4(y - 2) = 0, раскроем скобки.
2x + 12 - 4y + 8 = 0 и получаем общий вид уравнения:
2x - 4y + 20 = 0 можно сократить на 2:
x - 2y + 10 = 0.
б) если вектор нормали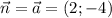
, то уравнение прямой имеет
вид: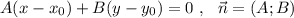
.
a) если вектор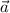
- это направляющий вектор 
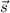, то каноническое уравнение прямой имеет вид: