Войти Регистрация Спроси ai-bota

Знайдіть площу фігури , симетричної фігурі x^2-4x+y^2-6y=1 відносно початку координат
ів Найдите площадь внешней, симметричной действия x ^ 2-4x + y ^ 2-6y = 1 существенно заданный координат

Показать ответ

Ответ:

semachelovekgood2

14.10.2020 12:05

$14\pi$

Объяснение:

Преобразуем уравнение фигуры:

$x^{2} - 4x + y^{2} - 6y = 1\\\\(x^{2} - 4x + 4) - 4 + (y^{2} - 6y + 9) - 9 = 1\\\\(x - 2)^{2} + (y - 3)^{2} - 13 = 1\\\\(x - 2)^{2} + (y - 3)^{2} = 14\\\\(x - 2)^{2} + (y - 3)^{2} = (\sqrt{14})^{2}$

Данное уравнение задает окружность с центром в точке (2;3) и радиусом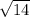 $\sqrt{14}$ , значит симметричная фигура - это окружность с центром в точке (-2; -3) и радиусом

Фактически нужно найти площадь круга. По формуле площади круга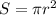 $S = \pi r^{2}$ найдем площади круга, ограниченного данной окружностью:

$S = \pi r^{2} = \pi (\sqrt{14} )^{2} = 14\pi$

Важно: уравнение окружности с центром в точке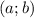 (a; b) и радиусом задается так:

$(x - a)^{2} + (y - b)^{2} = r^{2}$

0,0(0 оценок)

Популярные вопросы: Геометрия

veronikashows

01.01.2021 10:57

Объясните кто нибудь доказательство по второму признаку равенства треугольников. совсем не понимаю 7класс...

12qwerty97

25.09.2020 01:43

Периметр равнобренного треугольника равен 58см.основание больше боковой стороны на 7см.найдите боковую сторону...

tinyshbaev

09.02.2023 12:12

равнобокой трапеции меньшее основание равно 4 см, боковая сторона равна 6 см, острый угол равен 56°. Найдите большее основание трапеции. ответ дайте в сантиметрах....

layonel911

28.05.2022 00:02

равнобокой трапеции меньшее основание равно 4 см, боковая сторона равна 6 см,острый угол равен 56°. Найдите большее основание трапеции. ответ дайте в сантиметрах....

Danila251008

17.07.2021 17:44

В прямоугольном треугольнике один из острых углов равен 44º. Найдите два других угла. *...

Sashka15081

15.06.2021 20:04

На сторонах ab,bc,ac равнобедренного треугольника abc с основанием ac отмечены точки m,kи p соответственно так что...

DalinStreeet

06.01.2022 07:23

Найдите угол авс равнобедренной трапеции abcd, если диагональ ас образует с основанием ad и боковой стороной cd углы, равные 20° и 100° соответственно....

nastya09042

06.01.2022 07:23

Точка пересечения диагоналей трапеции делит одну из диагоналей на два отрезка длиной 4 см и 6 см. найдите длину большего основания трапеции, если длина меньшего основания равна 10...

dVioletta

31.03.2022 01:44

Вравнобедренный прямоугольный треугольник вписан квадрат так,что две его вершины находятся на гипотенузе, а другие две на катетах.найти сторону квадрата,если известно,что гипотенуза...

пидрила5

31.03.2022 01:44

Дан треугольник авс,угол с =90 градусов,катеты 3 см и 4 см.найдите r и r....

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку