Если все боковые грани наклонены к основанию под одинаковыми углами, то проекции высот боковых граней на основание - это радиусы r вписанной в основание окружности.
Высота основания к стороне 6 см равна √)5² - (6/2)²) = 4 см.
Площадь основания So = (1/2)*6*4 = 12 см².
Периметр основания Р = 2*5 + 6 = 16 см. полупериметр р = 16/2 = 8 см.
Радиус вписанной окружности r = S/p = 12/8 = 1,5 см.
Высота наклонной грани hн = r/cos 60° = 1.5/(1/2) = 3 см.
Площадь боковой поверхности Sбок = (1/2)Рhн = (1/2)*16*3 = 24 см².
Ну конечно в ЕГЭ нужно все подробно расписывать там по 1,2 признаку подобия и тд. Думаю, сам как нужно распишешь....
Проведем KO∥AA1
И сделаем проекцию KM на пл ABC
Это будет прямая OM
Рассмотрим плоскость основания, в нем проведем высоту BH-она делит основание AC пополам, так как по условию треугольник равнобедренный
Но тут не трудно заметить, что △AMO подобен △AHB с коэффициентом подобия равным 2. Значит MO∥BH и MO перпендикулярно AC
Теперь т о 3-х перпендикулярах. Если прямая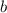
перпендикулярна проекции прямой на плоскость. То такая прямая 
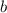перпендикулярна этой прямой.
У нас MO перпендикулярна AC значит по т о 3-х перпендикулярах KM перпендикулярна прямой AC ч.т.д
Если все боковые грани наклонены к основанию под одинаковыми углами, то проекции высот боковых граней на основание - это радиусы r вписанной в основание окружности.
Высота основания к стороне 6 см равна √)5² - (6/2)²) = 4 см.
Площадь основания So = (1/2)*6*4 = 12 см².
Периметр основания Р = 2*5 + 6 = 16 см. полупериметр р = 16/2 = 8 см.
Радиус вписанной окружности r = S/p = 12/8 = 1,5 см.
Высота наклонной грани hн = r/cos 60° = 1.5/(1/2) = 3 см.
Площадь боковой поверхности Sбок = (1/2)Рhн = (1/2)*16*3 = 24 см².
Sполн = 12 + 24 = 36 см².