Знайти площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, -7 см.
2. Знайти площу рівнобедриного трикутника, бічна сторона якого дорівнює 15 см, а а висота проведена до основи, -9 см.
3. Знайти площу ромба, сторона якого дорівнює 7√2 см, а один з кутів - 135°.
4. Знайти площу паралелограма, сторони якого дорівнюють 25 см і 7 см, а одна з діагоналей перпендикулярна до його сторони.
5. Знайти площу трапеції, основи якої дорівнюють 7 см і 9 см, а бічна сторона довжиною 6 см утворює з більшою основою кут 45°
1. 12 * 7 = 84 см"
2. 24 см
3.49√2 см
4. -----------
5.24√2 см²
Объяснение:
1. Тут и так понятно)
2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
225 = 81 +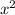
х =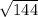 = 12 см
= 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Нехай РН=ТН=х см, тоді за теоремою Піфагора
х²+х²=6²; 2х²=36; х²=18; х=√18=3√2; РН=3√2 см.
S=(МР+КТ):2*3√2=(7+9)/2*3√2=24√2 см²