Геометрия: Знайти вертикальні кути якщо їх сума 130 градусів

Знайти вертикальні кути якщо їх сума 130 градусів

Показать ответ

Ответ:

Foxer30

29.01.2020 19:27

$\displaystyle OM=\frac{a}{4}$

Объяснение:

Дано: ΔАВС;

АК и СЕ - медианы;

СМ = МЕ; АО = ОК;

АС = а

Найти: ОМ.

1. СМ = МЕ; АО = ОК

Обратная теорема Фалеса: Если две или более прямых отсекают от двух других прямых равные или пропорциональные отрезки, то они параллельные. Утверждение справедливо, независимо от того, параллельные прямые или пересекаются.

⇒ ЕК || ОМ || АС

2. Рассмотрим АВС.

АЕ = ЕВ; СК = КВ (АК и СЕ - медианы)

⇒ ЕК - средняя линия (по определению)

Средняя линия равна половине основания.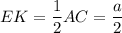

⇒ $\displaystyle EK = \frac{1}{2}AC=\frac{a}{2}$

3. Рассмотрим ΔАЕК.

АО = ОК; ОН || ЕК.

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок - средняя линия этого треугольника.

⇒ ОН - средняя линия ΔАЕК.

$\displaystyle OH=\frac{1}{2}EK=\frac{1}{2}*\frac{a}{2}=\frac{a}{4}$

4. Рассмотрим ΔЕКС.

СМ = МЕ; МР || ЕК;

⇒МР - средняя линия ΔЕКС.

$\displaystyle MP=\frac{1}{2}EK=\frac{1}{2}*\frac{a}{2}=\frac{a}{4}$

5. Рассмотрим ΔАЕС.

АН = НЕ (п.3); НМ || AC

⇒ НМ - средняя линия ΔАЕС.

$\displaystyle HM=\frac{1}{2}AC=\frac{1}{2}a=\frac{a}{2}$

6. Рассмотрим ΔАКС.

КР = РС (п.4); ОР || АС;

⇒ ОР - средняя линия ΔАКС.

$\displaystyle OP=\frac{1}{2}AC=\frac{1}{2}a =\frac{a}{2}$

$\displaystyle HM+OP=\frac{a}{2}+\frac{a}{2}HO+OM+OM+MP=a2OM =a-HO-MP2OM=a-\frac{a}{4}-\frac{a}{4}2OM=\frac{a}{2} OM=\frac{a}{4}$

Сторона треугольника равна а. Отрезок, соединяющий середины медиан, проведенных к двум другим сторон

0,0(0 оценок)

Ответ:

vakhram

10.11.2020 07:41

ответ: АВС=94 град Можно решить в двух вариантах.Можно решить в двух вариантах. В D А С Дано: ∆ АВС СD – биссектриса ∟АDС=112° ∟BCD=18° Найти: ∟ АВС = ? Решение: 1 вариант: ∆ АВС=180°= ∟ВАС+ ∟ АВС+ ∟ АСВ. Отсюда ∟ АВС = 180 – (∟ВАС+ ∟ АСВ) ∟BCD=∟АCD ∟ АСВ= ∟BCD+∟АCD Т.к. СD – биссектриса и делит ∟ АВС пополам, то ∟BCD=∟АCD=18°. Тогда ∟ АСВ=18+18=36°. ∟ВАС=∟DАC ∟DАC= 180 – (∟АCD+∟АDC)=180-(18+112)=50°. ∟ АВС=180-(50+36)=94° 2 вариант: ∟ АВС=∟CBD ∟CBD=180-(∟BCD+∟BDC) ∟BDC=180 -∟АDC (∟АDB –смежный угол) = 180-112=68° ∟CBD=180-(18+68)= 94°

0,0(0 оценок)

Популярные вопросы: Геометрия