1)Дано натуральное число. Вывести на экран все натуральные числа до заданного числа. 2)Вывести на экран кубы чисел от А до В (даны 2 числа, вывести все числа от А - первое введенное число до В - второе введенное число и возвести эти числа в степень 3)

1) 15342 2) 16034

Объяснение:

Для этого переведем его сначала в десятичную вот так :

1AE216 = 1∙16^3+10∙16^2+14∙16^1+2∙16^0 = 4096+2560+224+2 = 688210

Получилось: 688210

Переведем 688210 в восьмеричную систему вот так:

Целая часть числа находится делением на основание новой

(см. картинку)

Получилось: 688210(десятеричная) = 153428 (восьмеричная)

2)Для этого переведем его сначала в десятичную вот так :

1C1C16 = 1∙16^3+12∙16^2+1∙16^1+12∙16^0 = 4096+3072+16+12 = 719610

Получилось: 719610

Переведем 719610 в восьмеричную систему вот так:

Целая часть числа находится делением на основание новой

(см. картинку 2)

Получилось:719610 (десятеричная) = 160348 (восьмеричная)

Переведём 6882 из десятичной в восьмеричною систему счисления.

Переводить начинаем с наибольшего разряда.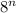 нужно подобрать наименьшее целое число n, чтобы значение

Методом подбора узнаем что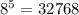 . Т.к. 6882 не равно 32768, то берём 4 степень, но чисел будет 5.

Первый разряд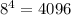 . Сколько раз можно взять 4096 из 6882? 1!

Первая цифра 1

1xxxx.

Отнимаем от 6882 один раз 4096 и получаем 2786

Следующий разряд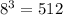 . Сколько раз можно взять 512 из 2786? 5!

Вторая цифра 5

15xxx

Отнимаем от 2786 пять раз 512 и получаем 226

Следующий разряд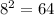 . Сколько раз из 226 можно взять 64? 3!

Третья цифра 3

153xx

Отнимаем от 226 три раза 64 и получаем 34

Следующий разряд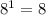 . Сколько раз 34 можно взять 8? 4!

Четвёртая цифра 4

1534x

Отнимаем от 34 четыре раза 8 и получаем 2

Последняя цифра - остаток, то есть 2

15342

Итак 1AE2 = 15342

2) 1C1C

Аналогично первому!

В десятичную: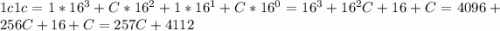

В восмеричную:

7196 - 4096 * 1 = 3100

1xxxx

3100 - 6 * 512 = 28

16xxx

28 - 0 * 64 = 28

160xx

28 - 3 * 8 = 4

1603x

4 - 4 * 1 = 0

16034