Верхняя строчка схемы Горнера представляет собой коэффициенты делимого многочлена:
1 | 0 | -15 | -10 | 24
В левый нижний угол схемы записывается из двучлена , на который делят многочлен, а в нижнюю строчку будем записывать коэффициенты многочлена, который получится после деления:
_| 1 | 0 | -15 | -10 | 24
1 | | | | |
Далее алгоритм работает следующим образом: в нижнюю строчку смещается первое число из верхней строчки, и число из нижней строчки умножается на , затем складывается со следующим числом в верхней строчке, и получившаяся сумма смещается вниз - и так до конца:
Пошаговое объяснение:
Верхняя строчка схемы Горнера представляет собой коэффициенты делимого многочлена:
1 | 0 | -15 | -10 | 24
В левый нижний угол схемы записывается
из двучлена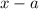 
, на который делят многочлен, а в нижнюю строчку будем записывать коэффициенты многочлена, который получится после деления:
_| 1 | 0 | -15 | -10 | 24
1 | | | | |
Далее алгоритм работает следующим образом: в нижнюю строчку смещается первое число из верхней строчки, и число из нижней строчки умножается на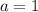
, затем складывается со следующим числом в верхней строчке, и получившаяся сумма смещается вниз - и так до конца:
_| 1 | 0 | -15 | -10 | 24
1 | 1 | 1 | -14 | -24 | 0
То есть получаем многочлен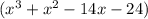
7
Пошаговое объяснение:
Посмотрим, как будут меняться последние цифры при возведении числа 2 в последовательные степени:
2^1 -> 2
2^2 -> 4
2^3 -> 8
2^4 -> 6
2^5 -> 2
То есть последняя цифра повторяется каждые четыре последовательные степени.
2^100 = 2^(4+96)=2^(4+4*24) -> 2^4 -> 6
Аналогично рассмотрим степени 3:
3^1 -> 3
3^2 -> 9
3^3 -> 7
3^4 -> 1
3^5 ->3
То есть опять через каждые четыре степени последняя цифра повторяется
3^100 = 3^(4+4*24) -> 3^4 -> 1
=> 2^100 + 3^100 -> 6+1 = 7