Пусть случайное событие — выбран качественный чайник, а гипотезы и — качественный чайник соответственно с первого, второго и третьего заводов. Тогда вероятность наступления события , если наступит конкретная гипотеза:
Пусть — коэффициент пропорциональности. Тогда и — поступление чайников из соответственно первого, второго и третьего заводов. Найдем по классической вероятности наступление гипотез:
Воспользуемся формулой полной вероятности наступления события
Тогда по формуле Байеса найдем вероятность того, что если чайник качественный, то он изготовлен на втором заводе:
Пусть случайное событие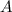 — выбран качественный чайник, а гипотезы
— выбран качественный чайник, а гипотезы 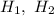 и
и 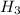 — качественный чайник соответственно с первого, второго и третьего заводов. Тогда вероятность наступления события
— качественный чайник соответственно с первого, второго и третьего заводов. Тогда вероятность наступления события 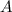 , если наступит конкретная гипотеза:
, если наступит конкретная гипотеза:
Пусть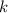 — коэффициент пропорциональности. Тогда
— коэффициент пропорциональности. Тогда 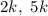 и
и 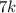 — поступление чайников из соответственно первого, второго и третьего заводов. Найдем по классической вероятности наступление гипотез:
— поступление чайников из соответственно первого, второго и третьего заводов. Найдем по классической вероятности наступление гипотез:
Воспользуемся формулой полной вероятности наступления события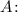
Тогда по формуле Байеса найдем вероятность того, что если чайник качественный, то он изготовлен на втором заводе:
ответ: 1) 0,66; 2) 0,38.
1) 0.66
2) 0.38
Пошаговое объяснение:
заводы поставляют чайники в соотношении 2: 5: 7 соответственно, значит всего 2+5+7=14 частей
Первый завод 2/14=1/7 часть всех чайников
Второй: 5/14
Третий: 7/14=1/2
Вероятность того, что чайник с первого завода качественный равна: 1-0,2=0,8
Вероятность того, что чайник со второго завода качественный равна: 1-0,3=0,7
Вероятность того, что чайник с третьего завода качественный равна: 1-0,4=0,6
1) А-чайник качественный.
Гипотезы:
H₁, H₂, H₃ - чайник изготовил 1, 2, 3 заводы соответственно.
P(H₁)=1/7; P(H₂)=5/14; P(H₃)=1/2
Условные вероятности:
A/H₁, A/H₂, A/H₃ - чайник качественный, при условии что его изготовил 1, 2, 3 заводы соответственно.
P(A/H₁)=0.8; P(A/H₂)=0.7; P(A/H₃)=0.6
Формула полной вероятности:
P(A)=P(H₁)*P(A/H₁)+P(H₂)*P(A/H₂)+P(H₃)*P(A/H₃)
2) Н₂/A - на втором заводе изготовили качественный чайник:
По формуле Байеса: