1. Даны две бесконечные арифметические прогрессии. Если к каждому члену одной прогрессии прибавить соответствующий член другой прогрессии, то будет ли полученная последовательность арифметической про- грессией?
2. Найдите сумму двадцати четырёх первых членов арифметической прогрессии (а ), если а -4,2, а разность прогрессии d = 0,6.
3. Найдите сумму сорока первых членов арифметической
прогрессии 14, 9, 4,
4. Арифметическая прогрессия (а ) задана формулой п-го члена а = 0,4n + 5. Найдите сумму тридцати шести n первых членов прогрессии.
5. Найдите сумму десяти первых членов арифметической
прогрессии (а ), если:
1) a, = 6, = 42;
2) a, = 45, a14 = -43.
6.
6. Найдите сумму семнадцати первых членов арифметической прогрессии (а ), если а = 84, а разность прогрессии d = 6,5.
7. Найдите сумму всех натуральных чисел, которые крат-
ны 9 и не больше 192.
8. Найдите первый и девятый члены арифметической прогрессии, если её разность равна -4, а сумма звенад- цати её первых членов равна 336.
9. Первый член арифметической прогрессии равен 16, а разность равна -4. Сколько надо взять первых членов прогрессии, чтобы их сумма была равной -324?

Показать ответ

Ответ:

liliaseeee

03.10.2020 14:55

За ознакою паралелограма, якщо пара протилежних сторин чотирикутника паралельни и ривни, то цей чотирикутник э паралелограмом. Якщо брати на озброэння векторний метод, то достатньо, щоб векторВС=векторАД.

Для цього знайдемо йих координати:

векторВС=(-5+6; 2-1)=(1;1),

векторАД=(4-3; -3+4)=(1;1).

Координати векторив спивпадають, отже, векторВС=векторАД ⇒АВСД - паралелограм, що и треба було довести.

P.S.: Щоб знайти координати вектора, вид координат кинця виднимають видповидни координати початку.

Подробнее - на -

Пошаговое объяснение:

0,0(0 оценок)

Ответ:

миру3

15.01.2021 18:10

$C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

или

$2\,\,753\,\,294\,\,408\,\,504\,\,640$

Пошаговое объяснение:

Давайте сначала введём понятие.

Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать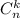 C^k_n и определим формулой

$\displaystyle C^k_n=\frac{n!}{k!(n-k)!}$

Если нужно доказательство, пишите

Итак, приступаем к решению.

Сначала раздаем первому игроку.

Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.

$\displaystyle C^{10}_{32}=\frac{32!}{10!(32-10)!}= \frac{22!*23*24*25*26*27*...*32}{22!*10*9*8*7*6*5*4*3*2} =\\=\frac{23*24*25*26*37*...*35}{10*9*8*7*6*5*4*3*2}=64512240$

Но можно было просто оставить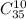 $C^{10}_{35}$

Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.

Тогда количество раздать второму 10 карт из 22 - это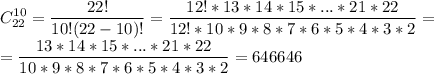 $\displaystyle C^{10}_{22}=\frac{22!}{10!(22-10)!}=\frac{12!*13*14*15*...*21*22}{12!*10*9*8*7*6*5*4*3*2}=\\=\frac{13*14*15*...*21*22}{10*9*8*7*6*5*4*3*2}=646646$

Или опять же можно было бы оставить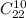 $C^{10}_{22}$

Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно

$\displaystyle C^{10}_{12}=\frac{12!}{10!(12-10)!}=\frac{12*11*10!}{10!*2}=66$

Ну хоть здесь нормальное число. Но опять же можно было и оставить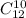 $C^{10}_{12}$

И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.

Получим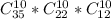 $C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

Или если в числах, то это

$64512240*646646*66=2753294408504640=2\,\,753\,\,294\,\,408\,\,504\,\,640$