1. Какие из нижеследующих выражений являются одночленами? Упражнения
r)
Д) clo.
в) а? - b;
г) -m;
m'm'm; 3) 0,6;
6
н) 1;
м) -34;
8.
а) 2,5x'у; б) а? + a;
10
е) -7xy ;
7
и)
ё) a8a;
ж) -2
13
2с
к) at 0,5);
о)
л) 3(x+y);
2. а) Напишите одночленс коэффициентом 14, переменнымиа, Бис, степенью 11.
Покажите его в виде произведения двух одночленов.
б) Напишите одночлен нестандартного вида с коэффициентом — 15, пере-
менными хи у, показателем степени 8. Представьте его в стандартном
в) Запишите любой одночлен стандартного вида и ему противоположный.
Виде.
56

ПОМАГИТЕ ОЧ НУЖНО​

Единственно возможный вариант - 17, 5.

Пошаговое объяснение:

Обозначим числа как и .

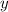Если сумма двух чисел - чётное число, то чётность искомых чисел одинакова, то есть или оба числа чётные или оба нечётные.

Но если числа одинаковой чётности, то разность будет тоже чётной. Между 10 и 14 только 1 чётное число - это 12, так как мы не считаем 10 и 14.

Теперь составляем систему уравнений:

Сложим уравнения:

Упростим правую часть:

Упростим левую часть:

И ещё раз её упростим:

Теперь легко найти :

Находим :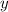

Вывод: Единственный возможный вариант - 17, 5.

ответ: 5 и 17.

Обозначим искомые числа за x и y. Тогда: x + y = 22.

Если сумма двух чисел - это четное число, то оба числа были одной и той же четности (то есть либо оба нечетные, либо оба четные).

Но и разность чисел одной четности - это тоже четное число. Поэтому x - y - это обязательно четное число. Но среди чисел меньше 14 и больше 10 только одно четное число, это 12 (считаем, что разность не может быть равна 10 и 14).

Тогда мы можем составить и решить эту систему уравнений:

Сложим эти уравнения:

Получается, Сережа загдал числа 5 и 17.

Примечание.

Если же все-таки сумма может быть равна 10 и 14, то роме этой пары еще подойдут пары (19, 5) и (17 и 7).