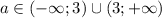1. Точки A, B, K и T — середины отрезков MF, PF, PN и MN соответственно, MP = 10 см, FN = 16 см .Определите вид четырёхугольника ABKT и вычислите его периметр. 2. Плоскость β пересекает стороны CF и CD треугольника CDF в точках M и N соответственно и параллельна стороне FD, MN = 6 см, FD = 21 см, MC = 10 см. Найдите сторону FC треугольника.
3. Треугольник ABC является изображением правильного треугольника A1B1C1. Постройте изображение центра описанной окружности треугольника A1B1C1 .

4. Плоскости α и β параллельны. Через точку D, находящуюся между этими плоскостями, проведены две прямые. Одна из них пересекает плоскости α и β в точках M1 и N1, а другая — в точках M2 и N2 соответственно. Найдите отрезок M1M2, если он на 8 см больше отрезка N1N2, N1M1=30 см, DN1 =5 см.

Показать ответ

Ответ:

иван2054

04.04.2021 22:22

4826390517

Пошаговое объяснение:

Числа 5 и 7 могут стоять только рядом с 0 или 1.

Поскольку 0 и 1 можно использовать только по одному разу, значит ответ должен либо начинаться одной из последовательностей:

7150*, 5170*, 7051*, 5071*

либо заканчиваться на:

*0517, *0715, *1507, *1705

Выберем только наименьшие из этих последовательностей. Остаётся два варианта: либо число начинается с 5071, либо заканчивается на 0517. Так, имеем два возможных варианта:

5071

0517

Число 9 может стоять рядом с 0, 1 и 3. Поскольку 0 и 1 мы уже использовали выше, значит 9 должна быть быть рядом:

50719

90517

Следующей цифрой может быть только 3:

507193

390517

Далее только 6:

5071936xxx

xxx6390517

За ней только 2:

50719362xx

xx26390517

У нас осталось две цифры: 4 и 8. Обе могут быть добавлены к результирующему числу в любом порядке. Очевидно, что 84 больше, чем 48, поэтому не будем рассматривать такой вариант. Прибавим 48:

5071936248

4826390517

Итого, мы получили 2 числа, удовлетворяющих условию задачи. Выберем среди них наименьшее. Это будет число 4826390517, что и является ответом к задаче.

0,0(0 оценок)

Ответ:

Fewfie

07.01.2023 16:04

$ax-2y-1=0\\-2y=-ax+1\\\\y=\dfrac{ax}2-\dfrac12\\\\y=\dfrac{ax}2-0.5\\\\y=\dfrac{a}2x-0.5$

$6x-4y-3=0\\-4y=3-6x\\4y=6x-3\\\\y=\dfrac64x-\dfrac34\\\\y=1.5x-0.75$

а) Если даны две функции, у которых коэффициент k (стоящий перед x) равен, то графики этих функций будут параллельны.

У первой функции k = a/2, у второй - 1,5. Для того, чтобы коэффициенты были равны, нужно подставить такое значение a, чтобы при делении на 2 оно давало 1,5.

В таком случае, a = 3.

б) Если даны две функции, не имеющих равных коэффициентов k и m (то есть она не будут параллельны или одна функция не равна другой), то у графиков этих функций будет одна общая точка. В таком случае, a может принять любое значение, кроме 3 (иначе графики будут параллельны).

То есть, $a\in(-\infty;3)\cup(3;+\infty)$