1. В правильной треугольной пирамиде SABC точки E, P, F –середины сторон BC, AB, AS. Определите вид сечения, проходящего через эти точки и найдите его площадь, если сторона основания пирамиды равна 8 см, а боковое ребро равно 20 см
1. Площадь квадрата равна длине его стороны, возведённой в квадрат: , где - это сторона квадрата. Зная площадь, можем вычислить длину стороны: см. Периметр квадрата равен длине его стороны, умноженной на 4: см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть, см. Составляем уравнение:
Тогда другая сторона его см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
Тогда площадь прямоугольника см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: , где - это сторона квадрата. Зная площадь, можем вычислить длину стороны: см. Периметр квадрата равен длине его стороны, умноженной на 4: см.
Пусть цифры данного числа х,у, z, t 1000x+100y+10z+t-1000t-100z-10y-x=909 999x+90y-90z-999t=909 поделим обе части равенства на 9 и сгруппируем 111(x-t)-10(z-y)=101 Это возможно, когда x-t=1, z-y=1 x=t+1, z=y+1 По условию сумма цифр числа делится на 9, т.е. x+y+z+t=9n, n - некоторое натуральное число t+1+y+y+1+t=9n 2(t+y+1)=9n, значит n=2, t+y=8 Переберем все цифры, сумма которых равна 8, зная зависимость переменных z и x от t и y , получим набор чисел
x y z t 8 1 2 7 7 2 3 6 6 3 4 5 5 4 5 4 4 5 6 3 3 6 7 2 2 7 8 1 9 0 1 8 Итого 8 чисел удовлетворяют условию задачи
1. Площадь квадрата равна длине его стороны, возведённой в квадрат: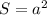 , где
, где  - это сторона квадрата. Зная площадь, можем вычислить длину стороны:
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: 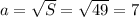 см. Периметр квадрата равен длине его стороны, умноженной на 4:
см. Периметр квадрата равен длине его стороны, умноженной на 4: 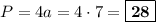 см.
см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть,
см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть, 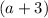 см. Составляем уравнение:
см. Составляем уравнение:
Тогда другая сторона его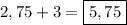 см.
см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда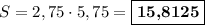 см².
см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
Тогда площадь прямоугольника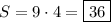 см².
см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: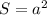 , где
, где  - это сторона квадрата. Зная площадь, можем вычислить длину стороны:
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: 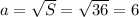 см. Периметр квадрата равен длине его стороны, умноженной на 4:
см. Периметр квадрата равен длине его стороны, умноженной на 4: 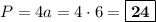 см.
см.
1000x+100y+10z+t-1000t-100z-10y-x=909
999x+90y-90z-999t=909 поделим обе части равенства на 9 и сгруппируем
111(x-t)-10(z-y)=101 Это возможно, когда x-t=1, z-y=1
x=t+1, z=y+1
По условию сумма цифр числа делится на 9, т.е. x+y+z+t=9n, n - некоторое натуральное число
t+1+y+y+1+t=9n
2(t+y+1)=9n, значит n=2, t+y=8
Переберем все цифры, сумма которых равна 8, зная зависимость переменных z и x от t и y , получим набор чисел
x y z t
8 1 2 7
7 2 3 6
6 3 4 5
5 4 5 4
4 5 6 3
3 6 7 2
2 7 8 1
9 0 1 8
Итого 8 чисел удовлетворяют условию задачи