Таки решил! 10sin 2x + 29sin x - 29cos x = 31 20sin x*cos x + 29sin x - 29cos x = 31 29(sin x - cos x) = 31 - 20sin x*cos x 29(sin x - cos x) = 10(sin^2 x + cos^2 x) - 20sin x*cos x + 21 29(sin x - cos x) = 10(sin x - cos x)^2 + 21
Замена sin x - cos x = y 10y^2 - 29y + 21 = 0 D = 29^2 - 4*10*21 = 841 - 840 = 1 y1 = sin x - cos x = (29 - 1)/20 = 28/20 = 7/5 y2 = sin x - cos x = (29 + 1)/20 = 30/20 = 3/2
Есть формула sin x - cos x = √2*(1/√2*sin x - 1/√2*cos x) = = √2*(sin x*cos(pi/4) - cos x*sin(pi/4)) = √2*sin(x - pi/4)
Находим х a) sin x - cos x = √2*sin(x - pi/4) = 7/5 sin(x - pi/4) = 7/(5√2) = 7√2/10 ~ 0,98995 < 1 x - pi/4 = (-1)^n*arcsin (7√2/10) + pi*n x = pi/4 + (-1)^n*arcsin (7√2/10) + pi*n
b) sin x - cos x = √2*sin(x - pi/4) = 3/2 sin(x - pi/4) = 3/(2√2) = 3√2/4 ~ 1,06066 > 1 Решений нет ответ: x = pi/4 + (-1)^n*arcsin (7√2/10) + pi*n
2) 6sin^2 x - 3sin x*cos x - cos^2 x = 1 = sin^2 x + cos^2 x 5sin^2 x - 3sin x*cos x - 2cos^2 x = 0 Делим все на cos^2 x 5tg^2 x - 3tg x - 2 = 0 Квадратное уравнение относительно tg x (tg x - 1)(5tg x + 2) = 0 a) tg x = 1; x = pi/4 + pi*k b) tg x = -2/5; x = -arctg(2/5) + pi*k
3) 3tg^2 x - 4cos^2 x = 8 3sin^2 x / cos^2 x - 4cos^2 x - 8 = 0 Умножаем все на cos^2 x 3sin^2 x - 4cos^4 x - 8cos^2 x = 0 3 - 3cos^2 x - 4cos^4 x - 8cos^2 x = 0 Замена cos^2 x = y, 0 <= y <= 1 при любом х 4y^2 + 11y - 3 = 0 (y + 3)(4y - 1) = 0 y1 = cos^2 x = -3 < 0 - решений нет y2 = cos^2 x = 1/4 a) cos x = -1/2; x1 = 2pi/3 + 2pi*k; x2 = 4pi/3 + 2pi*k b) cos x = 1/2; x3 = pi/3 + 2pi*n; x4 = -pi/3 + 2pi*n
4) 5sin 2x - 12(sin x - cos x) + 12 = 0 Решается также, как 1) 10sin x*cos x + 12 = 12(sin x - cos x) 10sin x*cos x - 5 + 17 = 12(sin x - cos x) -(5sin^2 x + 5cos^2 x - 10sin x*cos x) + 17 = 12(sin x - cos x) -5(sin x - cos x)^2 + 17 = 12(sin x - cos x)
Замена sin x - cos x = y. -5y^2 + 17 = 12y 5y^2 + 12y - 17 = 0 (y - 1)(5y + 17) = 0
y1 = sin x - cos x = √2*sin(x - pi/4) = 1 sin(x - pi/4) = 1/√2 x1 - pi/4 = pi/4 + 2pi*n; x1 = pi/2 + 2pi*n x2 - pi/4 = 3pi/4 + 2pi*n; x2 = pi + 2pi*n
y2 = sin x - cos x = √2*sin(x - pi/4) = -17/5 sin(x - pi/4) = -17/(5√2) = -17√2/10 ~ -2,404 < -1 Решений нет ответ: x1 = pi/2 + 2pi*n; x2 = pi + 2pi*n
Возьмём для простоты вычислений числа n-1, n, n+1. Пусть произведение этих чисел — это k-тая степень какого-то числа: . Зная, что два последовательных натуральных числа всегда взаимно простые, получаем, что число n взаимно простое с числами n-1, n+1, то есть n не имеет общих множителей в разложении с числами n-1 и n+1. Значит, каждый множитель n находится в k-той степени — само число n — это k-тая степень. Но тогда и (n-1)(n+1) = n²-1 является k-той степенью. Если возвести число n в квадрат, оно всё равно останется числом в степени k: . Но тогда n²-1 и n² — это два последовательных числа, являющиеся k-той степенью. Если взглянуть на графики степенных функций, становится ясно, что такого быть не может. Значит, и произведение трех последовательных натуральных чисел не является степенью натурального числа.
10sin 2x + 29sin x - 29cos x = 31
20sin x*cos x + 29sin x - 29cos x = 31
29(sin x - cos x) = 31 - 20sin x*cos x
29(sin x - cos x) = 10(sin^2 x + cos^2 x) - 20sin x*cos x + 21
29(sin x - cos x) = 10(sin x - cos x)^2 + 21
Замена sin x - cos x = y
10y^2 - 29y + 21 = 0
D = 29^2 - 4*10*21 = 841 - 840 = 1
y1 = sin x - cos x = (29 - 1)/20 = 28/20 = 7/5
y2 = sin x - cos x = (29 + 1)/20 = 30/20 = 3/2
Есть формула
sin x - cos x = √2*(1/√2*sin x - 1/√2*cos x) =
= √2*(sin x*cos(pi/4) - cos x*sin(pi/4)) = √2*sin(x - pi/4)
Находим х
a) sin x - cos x = √2*sin(x - pi/4) = 7/5
sin(x - pi/4) = 7/(5√2) = 7√2/10 ~ 0,98995 < 1
x - pi/4 = (-1)^n*arcsin (7√2/10) + pi*n
x = pi/4 + (-1)^n*arcsin (7√2/10) + pi*n
b) sin x - cos x = √2*sin(x - pi/4) = 3/2
sin(x - pi/4) = 3/(2√2) = 3√2/4 ~ 1,06066 > 1
Решений нет
ответ: x = pi/4 + (-1)^n*arcsin (7√2/10) + pi*n
2) 6sin^2 x - 3sin x*cos x - cos^2 x = 1 = sin^2 x + cos^2 x
5sin^2 x - 3sin x*cos x - 2cos^2 x = 0
Делим все на cos^2 x
5tg^2 x - 3tg x - 2 = 0
Квадратное уравнение относительно tg x
(tg x - 1)(5tg x + 2) = 0
a) tg x = 1; x = pi/4 + pi*k
b) tg x = -2/5; x = -arctg(2/5) + pi*k
3) 3tg^2 x - 4cos^2 x = 8
3sin^2 x / cos^2 x - 4cos^2 x - 8 = 0
Умножаем все на cos^2 x
3sin^2 x - 4cos^4 x - 8cos^2 x = 0
3 - 3cos^2 x - 4cos^4 x - 8cos^2 x = 0
Замена cos^2 x = y, 0 <= y <= 1 при любом х
4y^2 + 11y - 3 = 0
(y + 3)(4y - 1) = 0
y1 = cos^2 x = -3 < 0 - решений нет
y2 = cos^2 x = 1/4
a) cos x = -1/2; x1 = 2pi/3 + 2pi*k; x2 = 4pi/3 + 2pi*k
b) cos x = 1/2; x3 = pi/3 + 2pi*n; x4 = -pi/3 + 2pi*n
4) 5sin 2x - 12(sin x - cos x) + 12 = 0
Решается также, как 1)
10sin x*cos x + 12 = 12(sin x - cos x)
10sin x*cos x - 5 + 17 = 12(sin x - cos x)
-(5sin^2 x + 5cos^2 x - 10sin x*cos x) + 17 = 12(sin x - cos x)
-5(sin x - cos x)^2 + 17 = 12(sin x - cos x)
Замена sin x - cos x = y.
-5y^2 + 17 = 12y
5y^2 + 12y - 17 = 0
(y - 1)(5y + 17) = 0
y1 = sin x - cos x = √2*sin(x - pi/4) = 1
sin(x - pi/4) = 1/√2
x1 - pi/4 = pi/4 + 2pi*n; x1 = pi/2 + 2pi*n
x2 - pi/4 = 3pi/4 + 2pi*n; x2 = pi + 2pi*n
y2 = sin x - cos x = √2*sin(x - pi/4) = -17/5
sin(x - pi/4) = -17/(5√2) = -17√2/10 ~ -2,404 < -1
Решений нет
ответ: x1 = pi/2 + 2pi*n; x2 = pi + 2pi*n
Возьмём для простоты вычислений числа n-1, n, n+1. Пусть произведение этих чисел — это k-тая степень какого-то числа: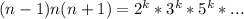
. Зная, что два последовательных натуральных числа всегда взаимно простые, получаем, что число n взаимно простое с числами n-1, n+1, то есть n не имеет общих множителей в разложении с числами n-1 и n+1. Значит, каждый множитель n находится в k-той степени — само число n — это k-тая степень. Но тогда и (n-1)(n+1) = n²-1 является k-той степенью. Если возвести число n в квадрат, оно всё равно останется числом в степени k: 
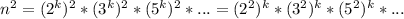. Но тогда n²-1 и n² — это два последовательных числа, являющиеся k-той степенью. Если взглянуть на графики степенных функций, становится ясно, что такого быть не может. Значит, и произведение трех последовательных натуральных чисел не является степенью натурального числа.