13. Определи в квадратных сантиметрах: 1) площадь квадрата ABCD; 2) площадь прямоугольника АЕРН; 3) площадь треугольника АЕН; 4) площадь квадрата HEFG; 5) площадь квадрата HKON; 6) площадь квадрата NKLM.
1) «Около любого ромба можно описать окружность.» — неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.
2) «В любой треугольник можно вписать не более одной окружности.» — верно, в любой треугольник можно вписать окружность, притом только одну.
3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.
4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
Пошаговое объяснение:
(-4,36-(2,56)):3-12*(-0,6)=(-6,92):3-(-7,2)=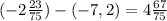
1) -4.36 - 2.56= - (4.36 + 2.56) = - 6.92
2) 12×(-0.6) = - 12×0.6 = - 7.2
3) -6.92÷3 = -6.92/3 = -692/300 = -173 · 4/75 · 4= -173/75 = -2·75 + 23/75 =-2 23/75 4) -2 23/75 - (-7.2) = -2 23/75+ 7.2 = -2 23/75+7 2/10 = 7 2/10 - 2 23/75 = 2 + 7·10/10 - 23 + 2·75/75 = 72/10 - 173/75 = 72·15/10·15 - 173·2/75·2 = 1080/150 - 346/150 = 1080 - 346/150 = 734/150 = 367 · 2/75 · 2 = 367/75 = 4·75 + 67/75 = 4 67/75Проверим каждое из утверждений.
1) «Около любого ромба можно описать окружность.» — неверно, чтобы около четырёхугольника можно было описать окружность, необходимо, чтобы сумма противоположных углов четырёхугольника составляла 180°. Это верно не для любого ромба.
2) «В любой треугольник можно вписать не более одной окружности.» — верно, в любой треугольник можно вписать окружность, притом только одну.
3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.
4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
ответ:2