18. Вопросы для самоконтроля. 1) Проведите примеры чисел:
а) натуральных;
б) целых;
в) дробных;
г) положительных;
д) отрицательных.
2) Какие числа называются рациональными? Приведите примеры.
3) Какая прямая называется координатной прямой? Как её построить? Что называется
Координатой точки?
4) Какие числа называются противоположными? Приведите примеры.
5) Какие числа называются взаимно простыми? Приведите примеры.
6) Какие числа называются взаимно обратными? Приведите примеры.
7) Дайте определение модуля рационального числа.
8) Чему равен модуль:
а) положительного числа;
б) отрицательного числа;
в) нуля?
9) Как сравнить рациональные числа на координатной прямой?
10) Как сравнить рациональные числа без использования координатной прямой?
Пошаговое объяснение:
Для вычисления интеграла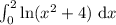 воспользуемся сначала методом интегрирования по частям:
воспользуемся сначала методом интегрирования по частям:
Заметим, что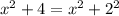 , и тогда в интеграле после интегрирования по частям напрашивается такая замена:
, и тогда в интеграле после интегрирования по частям напрашивается такая замена:
Если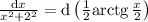 , то, положив
, то, положив 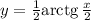 , найдём, что:
, найдём, что:
Применим это всё при вычислении получившегося интеграла.
Пределы интегрирования изменятся так:
Вычислим теперь сам интеграл:
Введём замену: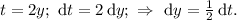
Пределы интегрирования изменятся так:
Продолжим вычисление интеграла:
Подставим найденное значение в выражение после интегрирования по частям и найдём итоговый результат:
Наконец, получаем, что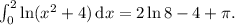
х и у - взаимно простые числа
a = 24 - коэффициент при переменной х
b = 36 - коэффициент при переменной у
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
24 | 2 36 | 2
12 | 2 18 | 2
6 | 2 9 | 3
3 | 3 3 | 3
1 1
24 = 2³ · 3 36 = 2² · 3²
НОД(a; b) = 2² · 3 = 12 - наибольший общий делитель
24х : 12 = 2х
36у : 12 = 3у
ответ: НОД (a; b) = 12.