(2 8 9х. найти: а) степень многочлена;
б) большой коэффициент и свободный член;
в) сумма коэффициентов многочлена;
г) сумма коэффициентов на четном уровне

Показать ответ

Ответ:

Vexicy

05.01.2023 00:29

$6\frac{2}{3}$

Пошаговое объяснение:

Коли функция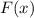 F(x) - первообразная для функции 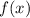f(x) , то функция производной от функции F(x) .

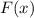Имея производную мы можем найти локальные максимумы и минимумы функции. Для этого найдем точки, в которых производная равняется 0.

f(x) = x^2 - x + 2 = 0

D = - 1 - 4 * 2 = -9 < 0 - уравнение не имеет действительных корней.

Значит функция монотонно убывающая или монотонно возрастающая.

Ветви параболы направлены вверх, значит функция монотонно возрастающая.

Также это означает, что максимальное и минимальные значения функция принимает на концах заданного отрезка - [0; 2].

F(0) - минимальное значение на отрезке. Значит F(2) - максимальное значение на отрезке [0; 2].

Вычислим это значение.

Для начала, найдем функцию F(x). Для этого проинтегрируем её производную:

$\int\limits y(x) \, dx = \int\limits x^2 - x + 2 \, dx = \frac{x^3}{3} - \frac{x^2}{2} + 2x + C$

Это выражение задаёт целое семейство функций, различающихся на C = const.

Теперь найдем среди этого семейства нужную нам функцию. По условию у нас дано частное значение функции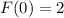 F(0) = 2

$\frac{0^3}{3} - \frac{0^2}{2} + 2*0 + C = 2\\C = 2$

$F(x) = \frac{x^3}{3} - \frac{x^2}{2} + 2x - 2$

Вычислим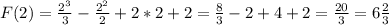 $F(2) = \frac{2^3}{3} - \frac{2^2}{2} + 2*2 + 2 = \frac{8}{3} - 2 + 4 + 2 = \frac{20}{3} = 6\frac{2}{3}$

0,0(0 оценок)

Ответ:

kirillarhipenc1

18.11.2022 16:14

324, 648.

Пошаговое объяснение:

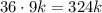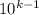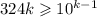Пусть в числе k цифр. Максимально возможная сумма цифр - это 9k, тогда само число не больше $36\cdot9k=324k$ . При этом само число не меньше $10^{k-1}$ . Чтобы был хоть какой-то шанс найти k-значное число, удовлетворяющее условию, должно быть выполнено неравенство $324k\geqslant10^{k-1}$ .

Правая часть неравенства растёт гораздо быстрее левой. Подбором находим, что при k = 4 неравенство выполнено, а при k = 5 уже нет. Докажем, что и при всех больших k неравенство не выполнено, по индукции:

База. k = 5: $1620=324\cdot5$ Переход. Пусть для всех 4 < k < n выполнено 324k

. Докажем, что и для k = n это так. Действительно, при n > 4 $10^{n-1}-324n=10\cdot10^{n-2}-324n10\cdot324(n-1)-324n=\\=2916n-32400$

Сумма цифр принимает значения вплоть до 36. Для сокращения перебора вспомним, что если число делится на 9 (а оно делится, так как делится на 36), то и сумма цифр должна делиться. Остаются 4 варианта:

Сумма цифр 9, тогда само число должно быть $36\cdot9=324$ . У него сумма цифр 9, подходит.Сумма цифр 18, само число $36\cdot18=648$ , сумма цифр правильная, подходит.Сумма цифр 27, само число $36\cdot27=972$ , не подходитСумма цифр 36, само число $36\cdot36=1296$ , не подходит.