423. Запишите натуральное число в виде смешанного. Заполните таблицу. 5 6 10 15 18 Натуральное число Смешанное со знаменателем 3 число со знаменателем 7

Показать ответ

Ответ:

Евабе

15.10.2020 05:52

Пошаговое объяснение:

для обоих случаев:

Площадь криволинейной трапеции - это определенный интеграл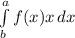 $\int\limits^a_b {f(x)x} \, dx$ для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.

f(x) = 6x -6x²; y=0; x=0; x=1

$f'(x) = -6\int\limits^0_1 {x^{2} } \, dx + 6 \int\limits^0_1 {} \, dx =$

(-2x³) Ι₀¹ + 3x²Ι₀¹ = -2 +3 = 1

$S_{G} = 1$

точки для построения графика

х=0; у= 0;

х= 0,2; у=0.96

х= 0,4; у = 1,44

х=0,6; у=1,44

х=0,8; у = 0,96

х = 1; у= 0

f(x) = х³ - 1; y=0; x=2; x=3

$f'(x) = \int\limits^2_3{x^{3} } \, dx - \int\limits^2_3 {} \, dx =$

(х⁴/4) Ι₂³ + (-х) Ι₂³ = 65/4 -1 = 61/4

$S_{G} = \frac{61}{4}$

точки для построения графика

х=2; у=7

х=2,2; у = 9,65

х = 2,4; у=14,62

х=2,6; у=16,58

х=2,8; у=20,95

х=3; у=26

Графики на фото.

файл 11 - график f(x) = 6x -6x²; y=0; x=0; x=1

файл 22 - график f(x) = х³ - 1; y=0; x=2; x=3

А) Вычислить площадь криволинейной трапеции, ограниченной линиями: у=6х-6х^2 , у=0, х=0,х=1. Сделать

0,0(0 оценок)

Ответ:

ivanermilov200

07.09.2020 12:46

Відповідь:

18 ОЛІВЦІВ.

Покрокове роз'яснення:

Це завдання перевіряє вміння розв'язувати елементарні задачі з теми "Теорія ймовірностей".

1) Відомо, що формула ймовірності події має вигляд: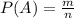 $P(A)=\frac{m}{n}$ , де A - подія; P(A) - ймовірність цієї події; n - кількість вcix можливих елементарних подій, а m - кількість елементарних подій, сприятливих А.

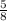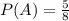2) Думаємо так: $\frac{5}{8}$ - це ймовірність події витягнути одну ручку, нехай A - це ця подія, тоді $P(A)=\frac{5}{8}$ .

3) Відомо, що олівців на 12 менше ніж ручок. Це означає, що якщо олівців є x (штук), то ручок тоді: x+12 (штук).

4) Захотівши один раз витягнути одну ручку, ви витягнете її, згідно умови, із олівців та всіх ручок, які є. Всього предметів у шухляді є лише ручки та олівці, тобто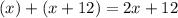 (x)+(x+12)=2x+12 - це кількість усіх предметів у шухляді.

5) Що таке ймовірність події витягнути одну ручку? - Це відношення кількості усіх подій "витягування ручки із шухляди" до "кількості усіх подій". Події "витягування ручки із шухляди" - це ті події, які сприяють появі події витягування одної ручки, тобто появі події, ймовірність якої дорівнює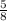 $\frac{5}{8}$ . Тобто сприятливі події - це ті події, які задаються формулою x + 12

6) Знаючи, що ймовірність витягнути одну ручку дорівнює 5/8, тобто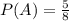 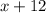$P(A) = \frac{5}{8}$ ; x+12 - це сприятливі події до події A (m), а 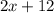2x+12 - це кількість усіх подій (n), то складемо рівність опираючись на пункт 1 і знайдемо x, що і буде відповіддю на наше завдання: