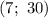Найдем стационарные (критические) точки. Для этого приравняем производную к нулю:
Следовательно, абсцисса — возможно, абсцисса точки экстремума — точка, при переходе через которую производная меняет знак. Если производная меняет знак с "–" на "+", то это точка минимума, если производная меняет знак с "+" на "–", то это точка максимума.
Рассмотрим промежуток :
Возьмем, например, абсциссу и подставим ее в производную:
Рассмотрим промежуток :
Возьмем, например, абсциссу и подставим ее в производную:
Следовательно, — абсцисса точки экстремума, а именно абсцисса точки минимума, так как производная меняет знак с "–" на "+". Тогда значение ординаты
а) 1 км = 1000 м
15 м от 1 км = 15/1000 км = 3/200 км - сократили на 5
б) 1 ч = 60 мин
20 мин от 1 ч = 20/60 ч = 1/3 ч - сократили на 20
в) 1 м = 100 см
10 см от 1 м = 10/100 м = 1/10 м - сократили на 10
г) 1 т = 1000 кг
75 кг от 1 т = 75/1000 т = 3/40 т - сократили на 25
д) 1 ц = 100 кг
30 кг о 1 ц = 30/100 ц = 3/10 ц - сократили на 10
е) 1 мин = 60 с
17 с от 1 мин = 17/60 мин
ж) 1 ч = 60 мин · 60 с = 3 600 с
10 с от 1 ч = 10/3600 ч = 1/360 ч - сократили на 10
з) 1 м = 100 см · 10 мм = 1000 мм
40 мм от 1 м = 40/1000 м = 1/25 м - сократили на 40
ОДЗ: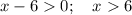
Найдем производную для заданной функции:
Найдем стационарные (критические) точки. Для этого приравняем производную к нулю:
Следовательно, абсцисса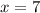 — возможно, абсцисса точки экстремума — точка, при переходе через которую производная меняет знак. Если производная меняет знак с "–" на "+", то это точка минимума, если производная меняет знак с "+" на "–", то это точка максимума.
— возможно, абсцисса точки экстремума — точка, при переходе через которую производная меняет знак. Если производная меняет знак с "–" на "+", то это точка минимума, если производная меняет знак с "+" на "–", то это точка максимума.
Рассмотрим промежуток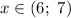 :
:
Возьмем, например, абсциссу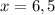 и подставим ее в производную:
и подставим ее в производную:
Рассмотрим промежуток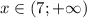 :
:
Возьмем, например, абсциссу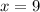 и подставим ее в производную:
и подставим ее в производную:
Следовательно,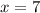 — абсцисса точки экстремума, а именно абсцисса точки минимума, так как производная меняет знак с "–" на "+". Тогда значение ординаты
— абсцисса точки экстремума, а именно абсцисса точки минимума, так как производная меняет знак с "–" на "+". Тогда значение ординаты 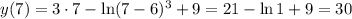
ответ: точка