5. В числовом наборе наименьшее значение равно 2, а наибольшее равно 9. Может ли среднее арифметическое такого набора быть равно: а) 6; б) 1; в) 9? Если может, приведите пример такого набора, если нет, то объясните, почему.
Если бы эскалатор остановился, оба бы одинаковое количество ступеней, просто один сделал бы это быстрее, а другой медленнее. Но эскалатор двигается, и тем самым отбирает часть ступенек у того и другого. У быстро идущего он успеет отобрать меньше, чем у медленно идущего. Вывод: быстро идущий насчитает больше ступеней, чем медленно идущий.
Для лучшего понимания можно применить такой прием: можно считать, что эскалатор неподвижен, но зато снизу им навстречу со скоростью эскалатора идет третий человек. Быстро идущий до встречи с ним пройдет больший путь, чем медленно идущий (ведь к моменту встречи путь быстрого идущего и идущего навстречу, как и путь медленно идущего и идущего навстречу, суммарно равны длине эскалатора). А количество ступеней пропорционально пройденному пути.
5.
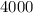кг бавовни-сирцю треба взяти, щоб отримати 960 кг волокна.
6.
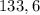км - шлях, який проїхали туристи за два дні.
7.
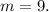
Пошаговое объяснение:
5. З бавовни-сирцю отримують 24 % волокна. Скільки треба взяти бавовни-сирцю, щоб отримати 960 кг волокна?
Сирця x кг - 100%
Волокна 960 кг - 24%
Вирішуємо пропорцію, знаючи її основну властивість: добуток крайніх членів дорівнює добутку середніх:
6. Першого дня туристи проїхали 72,5 км, що на 11,4 км більше, ніж другого. Який шлях проїхали туристи за два дні?
7. Середнім арифметичним чисел m і 12,6 є число 10,8. Знайдіть m.
Середнє арифметичне чисел — сума всіх чисел, поділена на їхню кількість:
Если бы эскалатор остановился, оба бы одинаковое количество ступеней, просто один сделал бы это быстрее, а другой медленнее. Но эскалатор двигается, и тем самым отбирает часть ступенек у того и другого. У быстро идущего он успеет отобрать меньше, чем у медленно идущего. Вывод: быстро идущий насчитает больше ступеней, чем медленно идущий.
Для лучшего понимания можно применить такой прием: можно считать, что эскалатор неподвижен, но зато снизу им навстречу со скоростью эскалатора идет третий человек. Быстро идущий до встречи с ним пройдет больший путь, чем медленно идущий (ведь к моменту встречи путь быстрого идущего и идущего навстречу, как и путь медленно идущего и идущего навстречу, суммарно равны длине эскалатора). А количество ступеней пропорционально пройденному пути.