584, 1) Построить угол KMN, равный 60°. Провести луч MP, который
разделит данный угол на два равНЫХ Угла. Такой луч называется биссектрисой угла

Показать ответ

Ответ:

546546YGygY

05.12.2021 01:15

ответ:1) 42) -23) -2Пошаговое объяснение:1. $\dfrac{\lg81}{\lg3}$ 1) По формуле перехода к новому основанию $\log_ab=\dfrac{\log_cb}{\log_ca}$

в данном случае а = 3, b = 81, c = 10

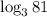
$\log_381$

2) Представим 81 как 3⁴ $\log_33^4$ 3) Вынесем степень как множитель $\log_ab^c=c\cdot\log_ab$

в данном случае а = 3, b = 3, c = 4

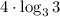
$4\cdot\log_33$

4) Заменим логарифм $\log_aa=1$

в данном случае а = 3

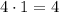
$4\cdot1=4$

ОТВЕТ 42. $\log_34-\log_316+\log_3\dfrac49$ 1) По формуле $\log_ab-\log_ac=\log_a\dfrac bc$

в данном случае а = 3, b = 4, c = 16

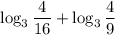
$\log_3\dfrac4{16}+\log_3\dfrac49$

2) По формуле $\log_ab+\log_ac=\log_abc$

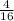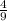
в данном случае а = 3, b = $\frac4{16}$ , с = $\frac49$

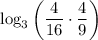
$\log_3\bigg(\dfrac4{16}\cdot \dfrac49\bigg)$

3) Посчитаем $\log_3\bigg(\dfrac{4\cdot4}{16\cdot9}\bigg)=\log_3\dfrac{16}{16\cdot9}=\log_3\dfrac19$ 4) Заменим $\dfrac19$ на 3⁻² $\log_33^-^2$ 5) Вынесем степень как множитель $\log_ab^c=c\cdot\log_ab$

в данном случае а = 3, b = 3, c = -2

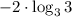
$-2\cdot\log_33$

6) Заменим логарифм $\log_aa=1$

в данном случае а = 3

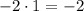
$-2\cdot1=-2$

ОТВЕТ -23. $2\log_727-\log_781-2\log_721$ 1) Занесем множитель как степень $c\cdot\log_ab=\log_ab^c$

в данном случае c = 2, a = 7, b = 27

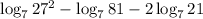
$\log_727^2-\log_781-2\log_721$

2) Занесем множитель как степень $c\cdot\log_ab=\log_ab^c$

в данном случае c = 2, a = 7, b = 21

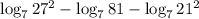
$\log_727^2-\log_781-\log_721^2$

3) По формуле $\log_ab-\log_ac=\log_a\dfrac bc$

в данном случае а = 7, b = 27², c = 81

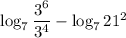
$\log_7\dfrac{3^6}{3^4}-\log_721^2$

5) Сократим дробь $\log_73^2-\log_721^2$ 6) По формуле $\log_ab-\log_ac=\log_a\dfrac bc$

в данном случае а = 7, b = 3², c = 21²

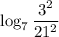
$\log_7\dfrac{3^2}{21^2}$

7) Сократим дробь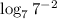 $\log_7\dfrac{3^2}{21^2}=\log_7\dfrac{3^2}{3^2\cdot7^2}=\log_7\dfrac1{7^2}$ 8) Заменим $\dfrac1{7^2}$ на 7⁻²

$\log_77^-^2$

9) Вынесем степень как множитель $\log_ab^c=c\cdot\log_ab$

в данном случае а = 7, b = 7, c = -2

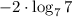
$-2\cdot\log_77$

10) Заменим логарифм $\log_aa=1$

в данном случае а = 7

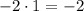
$-2\cdot1=-2$

ОТВЕТ -2

0,0(0 оценок)

Ответ:

lyntik228

05.06.2022 23:21

См. "Пошаговое объяснение".

Пошаговое объяснение:

1) Так как две соседние стороны образуют с диагональю равные углы, то это значит, что все 4 угла между сторонами прямоугольника равны:

90° : 2 = 45° .

2) Действительно, противоположные стороны прямоугольника параллельны, а его диагональ для этих параллельных является секущей. Образуется две пары накрест лежащих углов, которые равны между собой.

3) Следовательно, диагональ такого прямоугольника разбивает его на 2 равнобедренных треугольника, в котором основанием является диагональ, а боковыми сторонами - стороны одинаковой длины.

Таким образом, данный прямоугольник является квадратом, что и требовалось доказать.

0,0(0 оценок)

Популярные вопросы: Математика