Далее заметим, что для любого верно . То есть верхнее ограничение выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Нужно уметь решать задачи и методов составления уравнения или даже системы уравнений, потому что могут предложить для решения задачу гораздо посложнее, которую в уме не решить. Пусть сыну х лет, отцу - y лет, а матери - z лет. Составим систему уравнений: х+y=40 x+z=36 y+z=60 Выразив х через y в первом уравнении (y=40-х) и z через y в третьем уравнении (z=60-y) и подставив во второе уравнение, получим: (40-y) + (60-y) = 36, откуда y=32. Это возраст отца. Возраст сына х=40-32=8, матери - (32-4)=60-32)=28. ответ: Сыну 8 лет, матери 28 лет, отцу 32 года.
Пошаговое объяснение:
Введем замену
; 
.
Уравнение примет вид
Далее заметим, что для любого
верно 
. То есть верхнее ограничение 
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения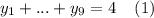 
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов
Пусть сыну х лет, отцу - y лет, а матери - z лет.
Составим систему уравнений:
х+y=40
x+z=36
y+z=60
Выразив х через y в первом уравнении (y=40-х) и z через y в третьем уравнении (z=60-y) и подставив во второе уравнение, получим: (40-y) + (60-y) = 36, откуда y=32. Это возраст отца. Возраст сына х=40-32=8, матери - (32-4)=60-32)=28.
ответ: Сыну 8 лет, матери 28 лет, отцу 32 года.