Пусть время первого х часов , второго у часов. Тогда производительность первого 1/x, второго 1/y. Вместе они работали 3 целых 3/5 часа = 18/5. Значит, совместная производительность 5/18. Первое уравнение 1/х + 1/у = 5/18
Второй сделал 1/3 работы за 1/3 : 1/у = у/3, первый сделал оставшуюся часть 2/3 работы зв 2/3 : 1/х =2х/3. Всего они работали 8 часов. Второе уравнение
2х/3 + у/3 = 8. Получили систему. Из первого уравнения 18x+18y=5xy, из второго
2x+y = 24. Отсюда, у = 24-2х. Подставим в первое, после упрощения получим:
5x^2 -69 +216 = 0, x=9, тогда у=24-18=6, т.е. время первого 9 часов, второго 6 часов
Или х=4,8 тогда у=14,4, т.е время первого 4,8 часа, второго 14,4 часа
Пусть - длина дуги, ограничивающей искомый сектор, вырезаемый из круглого листа.
Пусть - радиус круглого листа и одновременно образующая конуса (воронки).
Тогда радианная мера дуги , ограничивающей искомый сектор равна:
---------(1)
Нам необходимо найти при каком объем воронки (правильного конуса)
будет наибольшим. Запишем формулу объема конуса:
--------(2)
где - радиус основания конуса; - высота конуса
Поскольку длина окружности основания конуса равна , то отсюда
--------(3)
Высоту конуса найдем с теоремы Пифагора:
-------(4)
Подставим в (4) вместо выражение (3):
--------(5)
Подставим в (2) вместо и соотвественно выражения (3) и (5), получим:
--------(6)
где
Очевидно, что естественной областью определения объема как функции от есть интервал:
------(7)
Продифференцируем (6) по :
, отсюда
--------(8)
Чтобы функция (6) имела на естественной области ее определения максимум или минимум, необходимо чтобы --------(9)
Тогда из (8) и (9) получим:
, отсюда с учетом, что , найдем критическую точку:
, или
Поскольку естественной области определения (7) принадлежит только одна критическая точка и поскольку на естественной области определения функция (6) принимает только положительные значения, то критическая точка - точка максимума функции (6). Другими словами, при объем воронки будет наибольшим.
Теперь мы можем найти радианную меру искомого сектора, для чего подставим в (1) вместо критическую точку :
Пусть время первого х часов , второго у часов. Тогда производительность первого 1/x, второго 1/y. Вместе они работали 3 целых 3/5 часа = 18/5. Значит, совместная производительность 5/18. Первое уравнение 1/х + 1/у = 5/18
Второй сделал 1/3 работы за 1/3 : 1/у = у/3, первый сделал оставшуюся часть 2/3 работы зв 2/3 : 1/х =2х/3. Всего они работали 8 часов. Второе уравнение
2х/3 + у/3 = 8. Получили систему. Из первого уравнения 18x+18y=5xy, из второго
2x+y = 24. Отсюда, у = 24-2х. Подставим в первое, после упрощения получим:
5x^2 -69 +216 = 0, x=9, тогда у=24-18=6, т.е. время первого 9 часов, второго 6 часов
Или х=4,8 тогда у=14,4, т.е время первого 4,8 часа, второго 14,4 часа
Пусть - длина дуги, ограничивающей искомый сектор, вырезаемый из круглого листа.
- длина дуги, ограничивающей искомый сектор, вырезаемый из круглого листа.
Пусть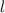 - радиус круглого листа и одновременно образующая конуса (воронки).
- радиус круглого листа и одновременно образующая конуса (воронки).
Тогда радианная мера дуги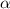 , ограничивающей искомый сектор равна:
, ограничивающей искомый сектор равна:
Нам необходимо найти при каком объем воронки (правильного конуса)
объем воронки (правильного конуса)
будет наибольшим. Запишем формулу объема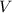 конуса:
конуса:
где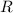 - радиус основания конуса;
- радиус основания конуса; 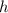 - высота конуса
- высота конуса
Поскольку длина окружности основания конуса равна , то отсюда
, то отсюда
Высоту конуса найдем с теоремы Пифагора:
Подставим в (4) вместо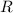 выражение (3):
выражение (3):
Подставим в (2) вместо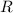 и
и 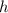 соотвественно выражения (3) и (5), получим:
соотвественно выражения (3) и (5), получим:
где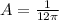
Очевидно, что естественной областью определения объема как функции от есть интервал:
есть интервал:
Продифференцируем (6) по :
:
Чтобы функция (6) имела на естественной области ее определения максимум или минимум, необходимо чтобы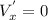 --------(9)
--------(9)
Тогда из (8) и (9) получим:
Поскольку естественной области определения (7) принадлежит только одна критическая точка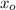 и поскольку на естественной области определения функция (6) принимает только положительные значения, то критическая точка
и поскольку на естественной области определения функция (6) принимает только положительные значения, то критическая точка 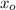 - точка максимума функции (6). Другими словами, при
- точка максимума функции (6). Другими словами, при 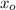 объем воронки будет наибольшим.
объем воронки будет наибольшим.
Теперь мы можем найти радианную меру искомого сектора, для чего подставим в (1) вместо критическую точку
критическую точку 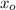 :
: