Автобус мав проїхати 280 км. Проїхавши 3/7 цієї відстані,автобус збільшив свою швідкість на 20 км у годину. Знайдить швідкість автобуса на кожній ділянці руху, якщо на весь шлях було витрачено 4 години

Показать ответ

Ответ:

karavanov1

26.06.2021 18:36

1. Поскольку из условия задачи нам известно, что обще число рабочих составляет 200 человек, следовательно при случайном выборе рабочего может попасться любой, а значит существует 200 разных исходов в данной ситуации.

2. А поскольку из условия задачи также известно, что норму не выполняют 15 из них, следовательно вариантов, удовлетворяющих требуемому условию 15. Вычислим какова вероятность того, что один случайно выбранный рабочий не выполняет норму.

р = 15 / 200 = 0,075.

3. А теперь вычислим вероятность того, что 2 случайно выбранных рабочих не выполняют норму.

р = 0,075 * 0,075 = 0,005625.

0,0(0 оценок)

Ответ:

Janna91

08.03.2021 16:59

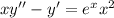
1) xy''-y'=e^xx^2

Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на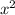 x^2 , получаем

$\dfrac{xy''-y'}{x^2}=e^x$

В левой части уравнения это ни что иное как формула производной частного, то есть :

$\left(\dfrac{y'}{x}\right)'=e^x$

$\dfrac{y'}{x}=\displaystyle \int e^xdx=e^x+C_1\\ \\ y'=xe^x+C_1x\\ \\ y=\int \Big(xe^x+C_1x)dx=\int xe^xdx+\int C_1xdx~\boxed{=}$

Подсчитаем отдельный интеграл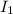 I_1 по частям.

$I_1=\displaystyle \int xe^xdx=\left|\left|\begin{array}{ccc}u=x;~~~ du=dx\\ \\ dv=e^xdx;~~ v=e^x\end{array}\right|\right|=uv-\int vdu=xe^x-\int e^xdx=\\ \\ \\ =xe^x-e^x+C_2$

$\boxed{=}~ xe^x-e^x+C_2+\dfrac{C_1x^2}{2}=e^x(x-1)+\dfrac{C_1x^2}{2}+C_2$

2) y''-3y'=0

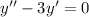
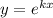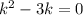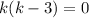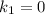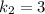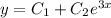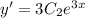Это линейное однородное дифференциальное с постоянными коэффициентами. Замена $y=e^{kx}$ , перейдём к характеристическому уравнению: k^2-3k=0 , k(k-3)=0 корни которого k_1=0 и k_2=3 . Тогда общее решение диф. уравнения: $y=C_1+C_2e^{3x}$ и его первая производная $y'=3C_2e^{3x}$ .