Айгүл бір стакан шырын , ал назар бір стакан сут сатып алды кімнің сатып алган заты кымбат ? каншага кымбат? есептин сызбасын тауып, есептеп шыгар

Показать ответ

Ответ:

yanakuzmina1

22.11.2022 15:51

ответ:функция не является непрерывной, в точках 1 и 2 она терпит разрывы второго родаПошаговое объяснение:Здесь единственные "плохие случаи" - это деление на 0. такое происходит при х = 2 или при х = 1 $f(x)=\dfrac{e^{\dfrac1{1-x}}}{x-2}$ 1. Рассмотрим точку 1

1. Тут явно разрыв, так как функция не определена

2. Вычислим односторонние пределы

$\displaystyle \lim_{x\to1-0}\dfrac{e^{\dfrac1{1-x}}}{x-2}=\lim_{x\to1-0}\dfrac1{x-2}\cdot\lim_{x\to1-0}e^{\dfrac1{1-x}}}=-\lim_{x\to1-0}e^{\dfrac1{1-x}}}=-\bigg(e^{\dfrac10}\bigg)=-\infty$

$\displaystyle \lim_{x\to1+0}\dfrac{e^{\dfrac1{1-x}}}{x-2}=\lim_{x\to1+0}\dfrac1{x-2}\cdot\lim_{x\to1+0}e^{\dfrac1{1-x}}}=1$

То есть функция сначала ушла в -∞ а затем резко появилась в 1

это разрыв второго рода

2. Рассмотрим точку 2

1. Тут опять разрыв, смотрим какой

2. Вычислим односторонние пределы

$\displaystyle \lim_{x\to2-0}\dfrac{e^{\dfrac1{1-x}}}{x-2}=\lim_{x\to2-0}\dfrac{1}{x-2}\lim_{x\to2-0}e^{\dfrac1{1-x}}=-\infty$

$\displaystyle \lim_{x\to2+0}\dfrac{e^{\dfrac1{1-x}}}{x-2}=\lim_{x\to2+0}\dfrac{1}{x-2}\lim_{x\to2+0}e^{\dfrac1{1-x}}=+\infty$

То есть функция сначала уходит в -∞ а потом выходит из +∞

В этой точке тоже разрыв второго рода

0,0(0 оценок)

Ответ:

миру3

15.01.2021 18:10

$C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

или

$2\,\,753\,\,294\,\,408\,\,504\,\,640$

Пошаговое объяснение:

Давайте сначала введём понятие.

Определение. Назовём числом сочетаний из n по k число выбрать из множества мощностью n элементов множество мощностью k элементов, будем обозначать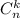 C^k_n и определим формулой

$\displaystyle C^k_n=\frac{n!}{k!(n-k)!}$

Если нужно доказательство, пишите

Итак, приступаем к решению.

Сначала раздаем первому игроку.

Для него есть 32 карты, из которых мы выбираем 10. Тогда количество выбрать эти карты есть число сочетаний из 32 по 10.

$\displaystyle C^{10}_{32}=\frac{32!}{10!(32-10)!}= \frac{22!*23*24*25*26*27*...*32}{22!*10*9*8*7*6*5*4*3*2} =\\=\frac{23*24*25*26*37*...*35}{10*9*8*7*6*5*4*3*2}=64512240$

Но можно было просто оставить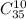 $C^{10}_{35}$

Мы уже дали 10 карт первому, поэтому осталось 32 - 10 = 22 карт.

Тогда количество раздать второму 10 карт из 22 - это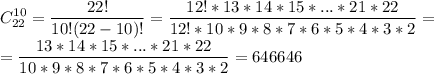 $\displaystyle C^{10}_{22}=\frac{22!}{10!(22-10)!}=\frac{12!*13*14*15*...*21*22}{12!*10*9*8*7*6*5*4*3*2}=\\=\frac{13*14*15*...*21*22}{10*9*8*7*6*5*4*3*2}=646646$

Или опять же можно было бы оставить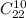 $C^{10}_{22}$

Третьему останется всего лишь 22 - 10 = 12 карт. Тогда точно также, число выбрать из 12 карт 10 равно

$\displaystyle C^{10}_{12}=\frac{12!}{10!(12-10)!}=\frac{12*11*10!}{10!*2}=66$

Ну хоть здесь нормальное число. Но опять же можно было и оставить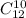 $C^{10}_{12}$

И так, для каждого из игроков есть свои варианты выбора, причем выбор другого, напрямую зависит от выбрав первого. Тогда нам необходимо перемножить все эти результаты.

Получим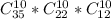 $C^{10}_{35}*C^{10}_{22}*C^{10}_{12}$

Или если в числах, то это

$64512240*646646*66=2753294408504640=2\,\,753\,\,294\,\,408\,\,504\,\,640$