Буду молится за вас днями и ночами, если мне

1) Так как призма правильня, то в основании лежит квадрат. АВСДА1В1С1Д1-данная призма. Из треугольника В1А1Д-прямоугольный, против угла в 30 градусов лежит кактет в 2 раза иеньше гиптенузы, следовательно сторона основания равна 2. Тогда, находим из треугольника ВСД по т. Пифагора ВД=корень из (4+4)=2корня из2

Из треугольника В1ВД находим ВВ1=корень из (16-8)=2корня из2

Тогда:

V=2*2*2корня из 2= 8корней из2

Радиус описанного около этой призмы цилиндра R=0.5BД=корень из2

Тогда его объем равен:

V=piR^2*BB1=4*pi*корень из2

Пошаговое объяснение:

Точка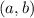 на комплексной плоскости изображает число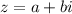

- действительная часть числа (Real)

- мнимая часть числа (Imaginary)

В соответствии с этим строим точки для 16.1. (Картинка 1)

Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.

Т.е. сопряженным для числа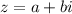 будет являться число .

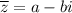В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).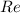

На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.