Пошаговое объяснение:
Так как в четвертом подъезде квартиры начинаются с 253, значит в первых трех подъездах 252 квартиры
252÷3=84 квартиры в каждом подъезде
84÷12=7 квартир на каждом этаже
1подьезд 1-84
2подъезд 85+84-1(квартира под номером 85)=169-1=168; 85-168
3подъезд 169+84-1=253-1=252; 169-252
4подъезд 253+84-1=337-1=336; 253-336
5подъезд 337+84-1=421-1=420; 337-420
6подъезд 421+84-1=505-1=504; 421-504
Значит искомая квартира находитсяв 6 подъезд
С 421 квартиры начинается 6 подъезд
1 этаж 421+7-1(квартира под номером 421)=428-1=427; 421-427
2 этаж 428+7-1=435-1=434; 428-434
3 этаж 435+7-1=442-1=441; 435-441
4 этаж 442+7-1=449-1=448; 442-448
5 этаж 449+7-1=456-1=455; 449-455
6 этаж 456+7-1=463-1=462; 456-462
7 этаж 463+7-1=470-1=469; 463-469
8 этаж 470+7-1=477-1=476; 470-476
9 этаж 477+7-1=484-1=483; 477-483
Искомая нами квартира находится на 9 этаже
Для всех равных пар натуральных чисел
Пусть канонические виды чисел x и y таковы:
где - простые числа, а
- целые неотрицательные степени простых чисел (некоторые могут равняться нулю).
Тогда по свойству НОД(x; y)=
где
По условию НОД(x; y)²=x · y и отсюда следует, что
Очевидно, что значение min(m; n) или m или n. Поэтому, если
, то из равенства следует, что и . Точно такое равенство можно установить если .
И такие равенства получаются для других степеней простых чисел.
Отсюда заключаем, что НОД(x; y)²=x · y, тогда и только тогда, когда x=y.
Отсюда следует ответ к задаче: для всех равных пар натуральных чисел.
Пошаговое объяснение:
Так как в четвертом подъезде квартиры начинаются с 253, значит в первых трех подъездах 252 квартиры
252÷3=84 квартиры в каждом подъезде
84÷12=7 квартир на каждом этаже
1подьезд 1-84
2подъезд 85+84-1(квартира под номером 85)=169-1=168; 85-168
3подъезд 169+84-1=253-1=252; 169-252
4подъезд 253+84-1=337-1=336; 253-336
5подъезд 337+84-1=421-1=420; 337-420
6подъезд 421+84-1=505-1=504; 421-504
Значит искомая квартира находитсяв 6 подъезд
С 421 квартиры начинается 6 подъезд
1 этаж 421+7-1(квартира под номером 421)=428-1=427; 421-427
2 этаж 428+7-1=435-1=434; 428-434
3 этаж 435+7-1=442-1=441; 435-441
4 этаж 442+7-1=449-1=448; 442-448
5 этаж 449+7-1=456-1=455; 449-455
6 этаж 456+7-1=463-1=462; 456-462
7 этаж 463+7-1=470-1=469; 463-469
8 этаж 470+7-1=477-1=476; 470-476
9 этаж 477+7-1=484-1=483; 477-483
Искомая нами квартира находится на 9 этаже
Для всех равных пар натуральных чисел
Пошаговое объяснение:
Пусть канонические виды чисел x и y таковы:
где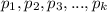 - простые числа, а
- простые числа, а
Тогда по свойству НОД(x; y)=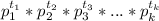
где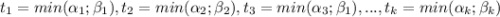
По условию НОД(x; y)²=x · y и отсюда следует, что
Очевидно, что значение min(m; n) или m или n. Поэтому, если
И такие равенства получаются для других степеней простых чисел.
Отсюда заключаем, что НОД(x; y)²=x · y, тогда и только тогда, когда x=y.
Отсюда следует ответ к задаче: для всех равных пар натуральных чисел.