Дана функция y=ƒ(x) и два значения аргумента x1 и x2. необходимо найти приближенное значение данной функции при x=x2, используя ее значение при x=x1 и заменяя прирост ∆y функции y=ƒ(x) соответствующим дифференциалом dy:
1) y=3√3x2+8x−16; x1=4; x2=3,94;
2) y=cos(x); x1=60◦; x2=63◦.
2) x1 = 60 (deg) = pi/3 = pi*1/3 (rad)
x2 = 63 (deg) = pi*7/20(rad)
производная от косинуса это минус синус
умножаем значение производной в точке x1 на прирост аргумента то есть x2-x1, и прибавляем полученное значение к значению функции в точке x1.
прирост значения функции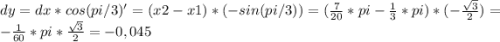 (приблизительно)
(приблизительно)